Statistical Inference
Bora Jin
Today's Goal
- Understand statistical process terminology
- Understand different types of conclusions we can make through statistical inference
- Understand point estimate and confidence intervals
Terminology
Population: a group of individuals or objects we are interested in studying
Parameter: a numerical quantity derived from the population (almost always unknown)
- Parameters could be the mean, median, correlation, maximum, etc.
If we had data from every unit in the population, we could just calculate population parameters and be done!
Terminology
Unfortunately, we usually cannot do this, so we draw conclusions from
Sample: a subset of our population of interest
Statistic: a numerical quantity derived from a sample
- Statistics could be the mean, median, correlation, maximum, etc.
Naturally, it makes sense to use the sample mean (and other quantities derived from the sample) to make generalizations about the population mean.
Statistical Inference
Statistical inference is the process of using sample data to make conclusions about the underlying population the sample came from.
Estimation: using the sample to estimate a plausible range of values for the unknown parameter
Testing: evaluating whether our observed sample provides evidence for or against some claim about the population
Statistical Inference
Statistical inference is the process of using sample data to make conclusions about the underlying population the sample came from.
Estimation: using the sample to estimate a plausible range of values for the unknown parameter
Testing: evaluating whether our observed sample provides evidence for or against some claim about the population
Today we will focus on Estimation.
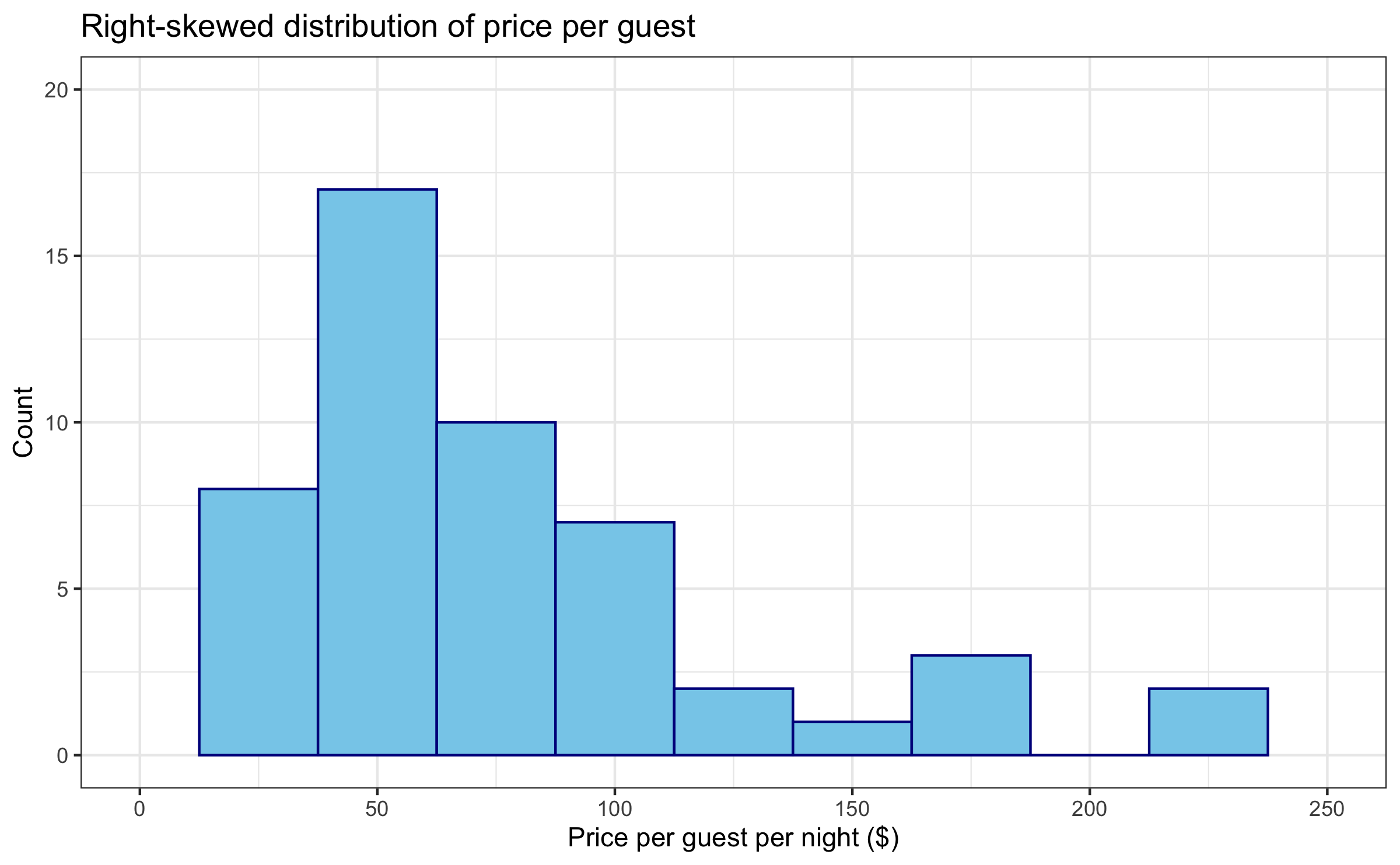
Asheville Airbnb
- Research question: What is the mean price per guest per night among Airbnb rentals with at least ten reviews in Asheville (zip codes 28801 - 28806)?
Asheville Airbnb
Research question: What is the mean price per guest per night among Airbnb rentals with at least ten reviews in Asheville (zip codes 28801 - 28806)?
Population of interest: listings in Asheville with at least ten reviews.
Asheville Airbnb
Research question: What is the mean price per guest per night among Airbnb rentals with at least ten reviews in Asheville (zip codes 28801 - 28806)?
Population of interest: listings in Asheville with at least ten reviews.
Parameter of interest: mean price per guest per night among these listings.
Asheville Airbnb
Research question: What is the mean price per guest per night among Airbnb rentals with at least ten reviews in Asheville (zip codes 28801 - 28806)?
Population of interest: listings in Asheville with at least ten reviews.
Parameter of interest: mean price per guest per night among these listings.
We have data on the price per guest (ppg) for a random sample of 50 Airbnb listings
with at least ten reviews in Asheville, NC, that were active on June 25, 2020 (Source: http://insideairbnb.com/).
Asheville Airbnb
Research question: What is the mean price per guest per night among Airbnb rentals with at least ten reviews in Asheville (zip codes 28801 - 28806)?
Population of interest: listings in Asheville with at least ten reviews.
Parameter of interest: mean price per guest per night among these listings.
We have data on the price per guest (ppg) for a random sample of 50 Airbnb listings
with at least ten reviews in Asheville, NC, that were active on June 25, 2020 (Source: http://insideairbnb.com/).
- Sample: randomly selected 50 listings in the Asheville with at least ten reviews.
Asheville Airbnb
Research question: What is the mean price per guest per night among Airbnb rentals with at least ten reviews in Asheville (zip codes 28801 - 28806)?
Population of interest: listings in Asheville with at least ten reviews.
Parameter of interest: mean price per guest per night among these listings.
We have data on the price per guest (ppg) for a random sample of 50 Airbnb listings
with at least ten reviews in Asheville, NC, that were active on June 25, 2020 (Source: http://insideairbnb.com/).
Sample: randomly selected 50 listings in the Asheville with at least ten reviews.
Statistic: mean price per guest per night among these sampled listings.
Point Estimate
A point estimate is a single value computed from the sample data to serve as the "best guess", or estimate, for the population parameter.
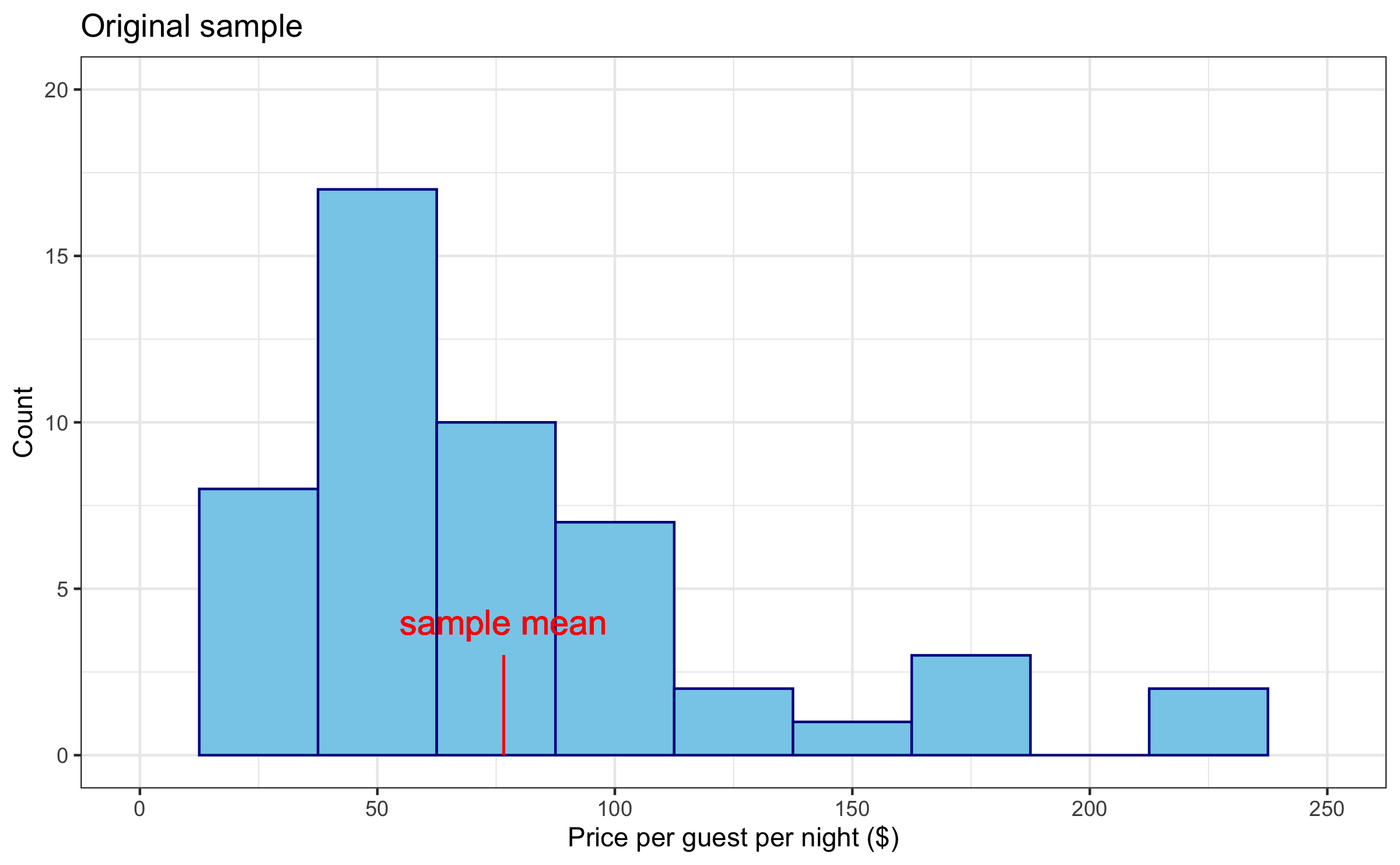
abb <- read_csv("data/asheville.csv")abb %>% summarize(mean_price = mean(ppg))## # A tibble: 1 × 1## mean_price## <dbl>## 1 76.6Point vs. Interval
If you want to estimate a population parameter, do you prefer to report a single value or a range of values the parameter might be in?


Point vs. Interval
If you want to estimate a population parameter, do you prefer to report a single value or a range of values the parameter might be in?


If we report a point estimate, we probably won’t hit the exact population parameter.
If we report a range of plausible values, we have a good shot at capturing the parameter.
Confidence Intervals
A plausible range of values for the population parameter is a confidence interval.
In order to construct a confidence interval we need to quantify variability (uncertainty) of our sample statistic.
For example, if we want to construct a confidence interval for a population mean, we need to come up with a plausible range of values around our observed sample mean.
This range will depend on how precise and how accurate our sample mean is as an estimate of the population mean.
Quantifying this requires a measurement of how much we would expect the sample mean to vary from sample to sample.
Quantifying Variability
- There is almost always some variability of sample statistics because random samples may differ from each other.
Quantifying Variability
There is almost always some variability of sample statistics because random samples may differ from each other.
If we took another random sample of 50 Airbnb listings in Asheville, we probably wouldn't get the same mean price per guest.
Quantifying Variability
There is almost always some variability of sample statistics because random samples may differ from each other.
If we took another random sample of 50 Airbnb listings in Asheville, we probably wouldn't get the same mean price per guest.
Suppose we split the class in half and ask each student their height. Then, we calculate the mean height of students on each side of the classroom. Would you expect these two means to be exactly equal, close but not equal, or wildly different?
Quantifying Variability
There is almost always some variability of sample statistics because random samples may differ from each other.
If we took another random sample of 50 Airbnb listings in Asheville, we probably wouldn't get the same mean price per guest.
Suppose we split the class in half and ask each student their height. Then, we calculate the mean height of students on each side of the classroom. Would you expect these two means to be exactly equal, close but not equal, or wildly different?
Suppose you randomly sample 50 students and 5 of them are left handed. If you were to take another random sample of 50 students, how many would you expect to be left handed? Would you be surprised if only 3 of them were left handed? Would you be surprised if 40 of them were left handed?
Quantifying Variability
We can quantify the variability of sample statistics using different approaches:
- Simulation: via bootstrapping or "resampling" techniques
or
- Theory: via the Central Limit Theorem
Quantifying Variability
We can quantify the variability of sample statistics using different approaches:
- Simulation: via bootstrapping or "resampling" techniques
or
- Theory: via the Central Limit Theorem
Today we will focus on Booststrapping.
Bootstrapping

The term bootstrapping comes from the phrase "pulling oneself up by one’s bootstraps", which is a metaphor for accomplishing an impossible task without any outside help.
Impossible task: Estimating a population parameter using data from only the given sample
Note: This notion of saying something about a population parameter using only information from an observed sample is the crux of statistical inference,
not limited to bootstrapping.
Bootstrappng Steps
- Take a bootstrap sample: a random sample taken with replacement from the original sample, of the same size as the original sample.
Bootstrappng Steps
Take a bootstrap sample: a random sample taken with replacement from the original sample, of the same size as the original sample.
Calculate the bootstrap statistic: the statistic you’re interested in (the mean, the median, the correlation, etc.) computed on the bootstrap sample.
Bootstrappng Steps
Take a bootstrap sample: a random sample taken with replacement from the original sample, of the same size as the original sample.
Calculate the bootstrap statistic: the statistic you’re interested in (the mean, the median, the correlation, etc.) computed on the bootstrap sample.
Repeat steps (1) and (2) many times to create a bootstrap distribution: a distribution of bootstrap statistics.
Bootstrappng Steps
Take a bootstrap sample: a random sample taken with replacement from the original sample, of the same size as the original sample.
Calculate the bootstrap statistic: the statistic you’re interested in (the mean, the median, the correlation, etc.) computed on the bootstrap sample.
Repeat steps (1) and (2) many times to create a bootstrap distribution: a distribution of bootstrap statistics.
Calculate the bounds of the XX% confidence interval as the middle XX% of the bootstrap distribution.
Step 1
Take a bootstrap sample: a random sample taken with replacement from the original sample, of the same size as the original sample.
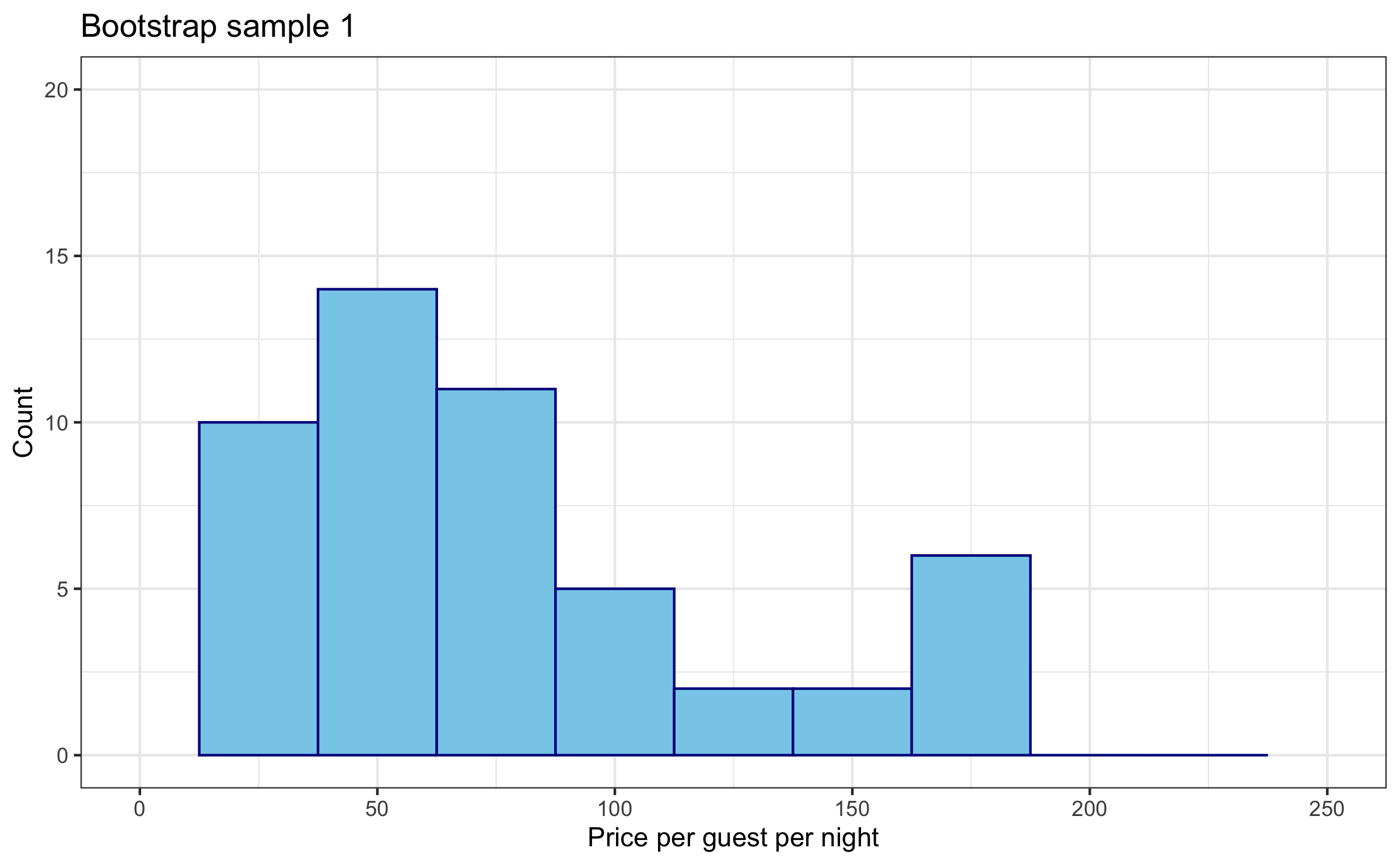
Step 2
Calculate the bootstrap statistic (in this case, the sample mean) using the bootstrap sample.
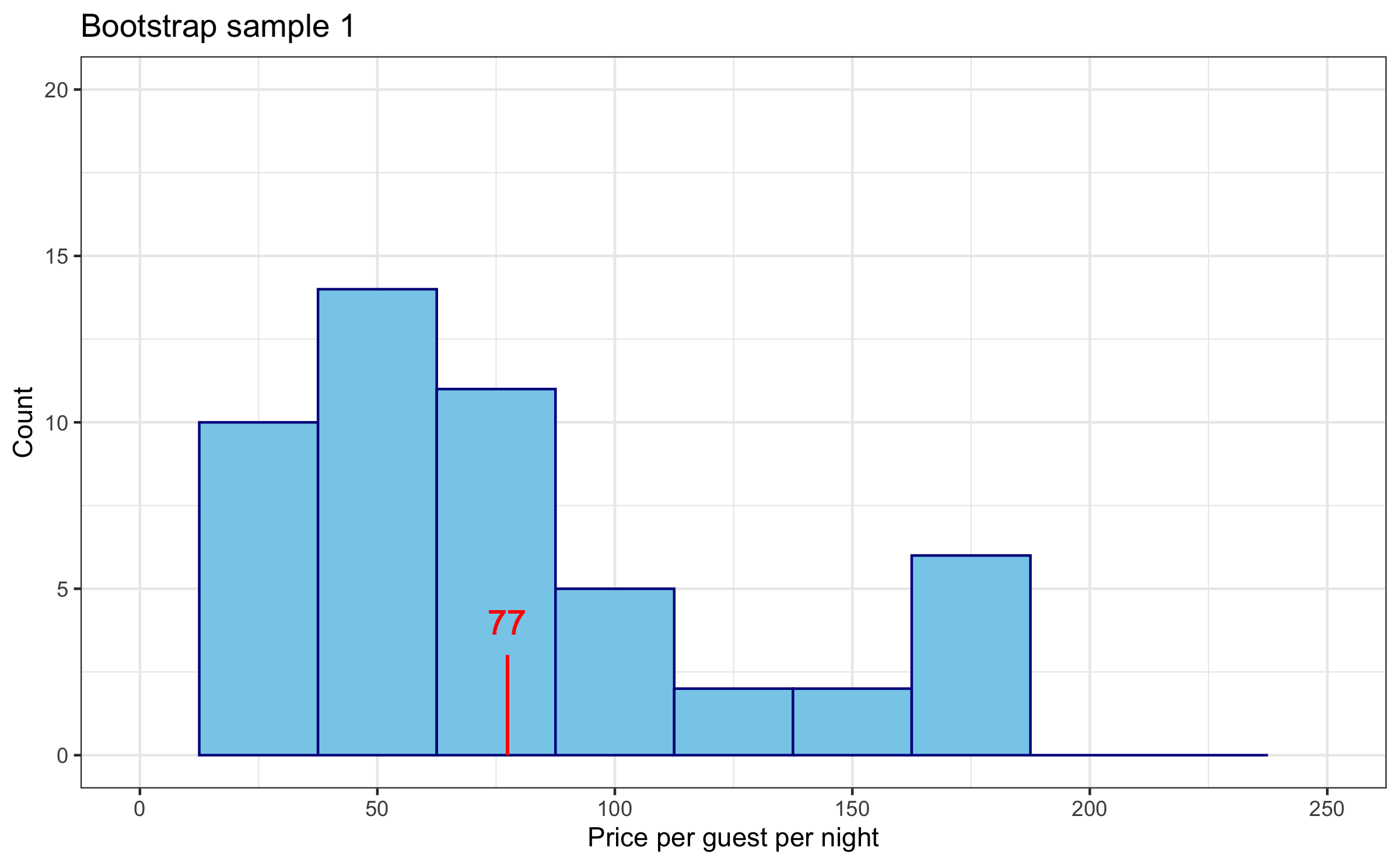
Step 3
Do steps 1 and 2 over and over again to create a bootstrap distribution of sample means.
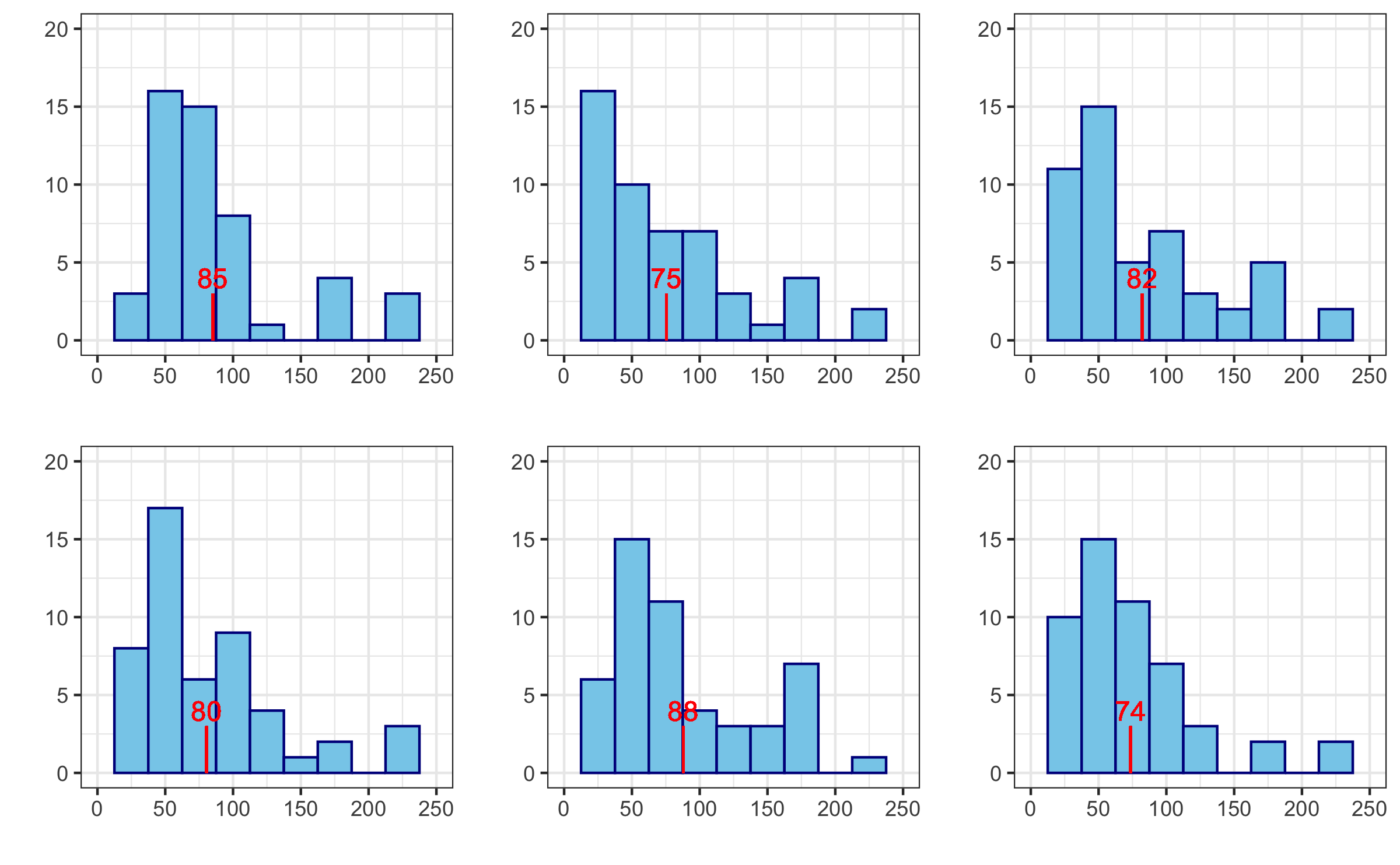
Step 3
In this plot, we've taken 1,000 bootstrap samples, calculated the sample mean for each, and plotted them in a histogram.
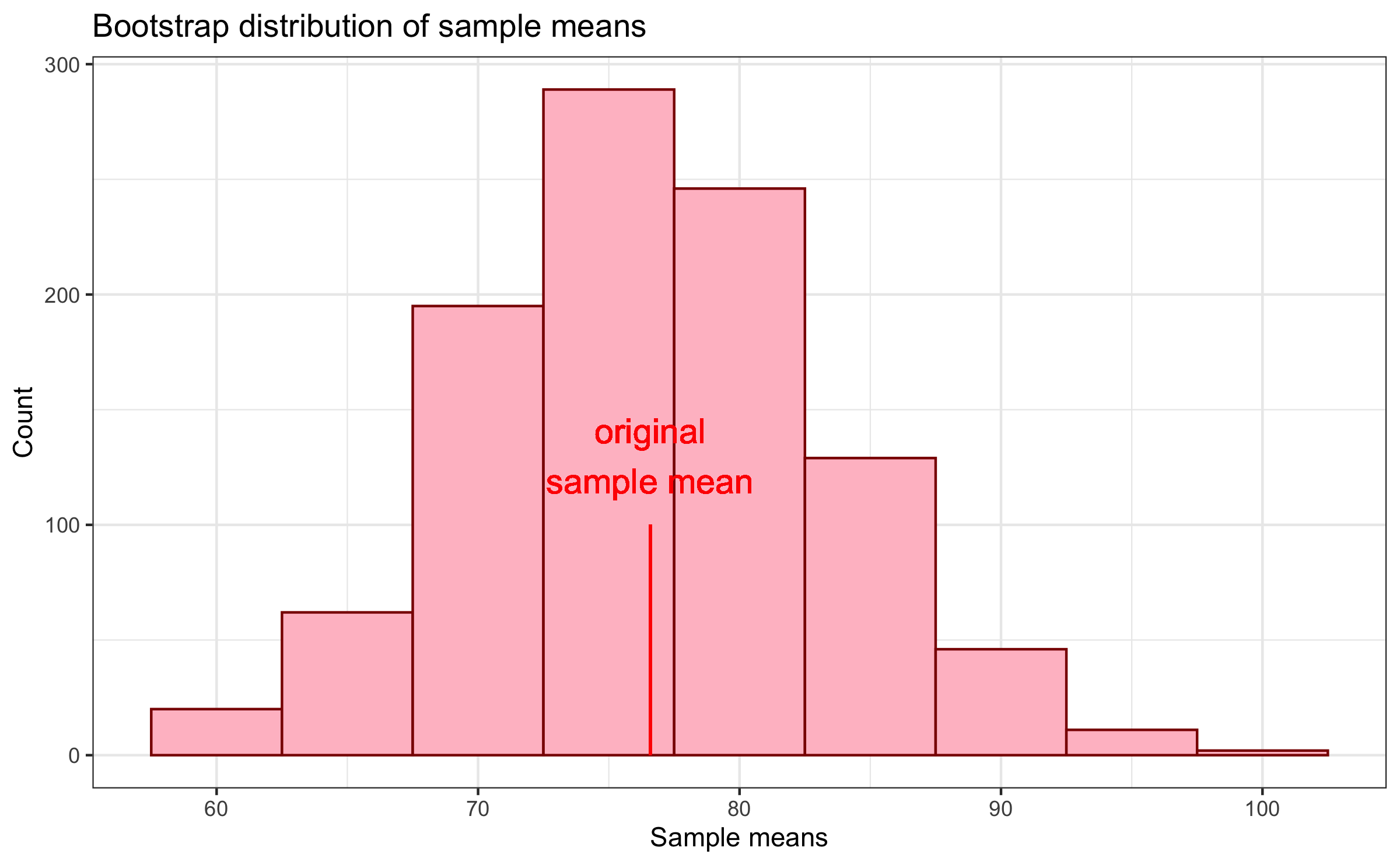
Step 3
Here we compare the bootstrap distribution of sample means to that of the original data. What do you notice?
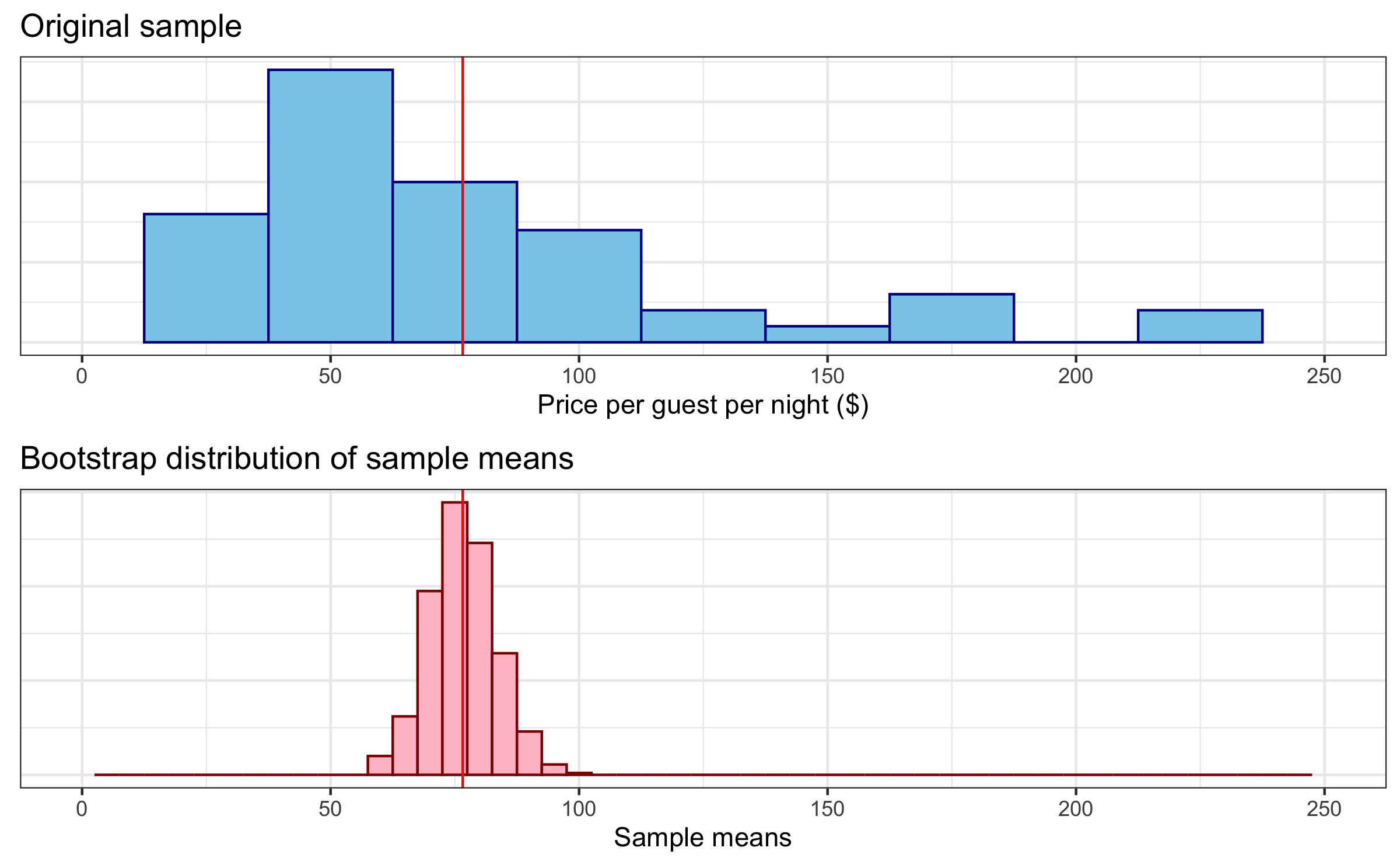
Step 4
Calculate the bounds of the bootstrap interval by using percentiles of the bootstrap distribution.
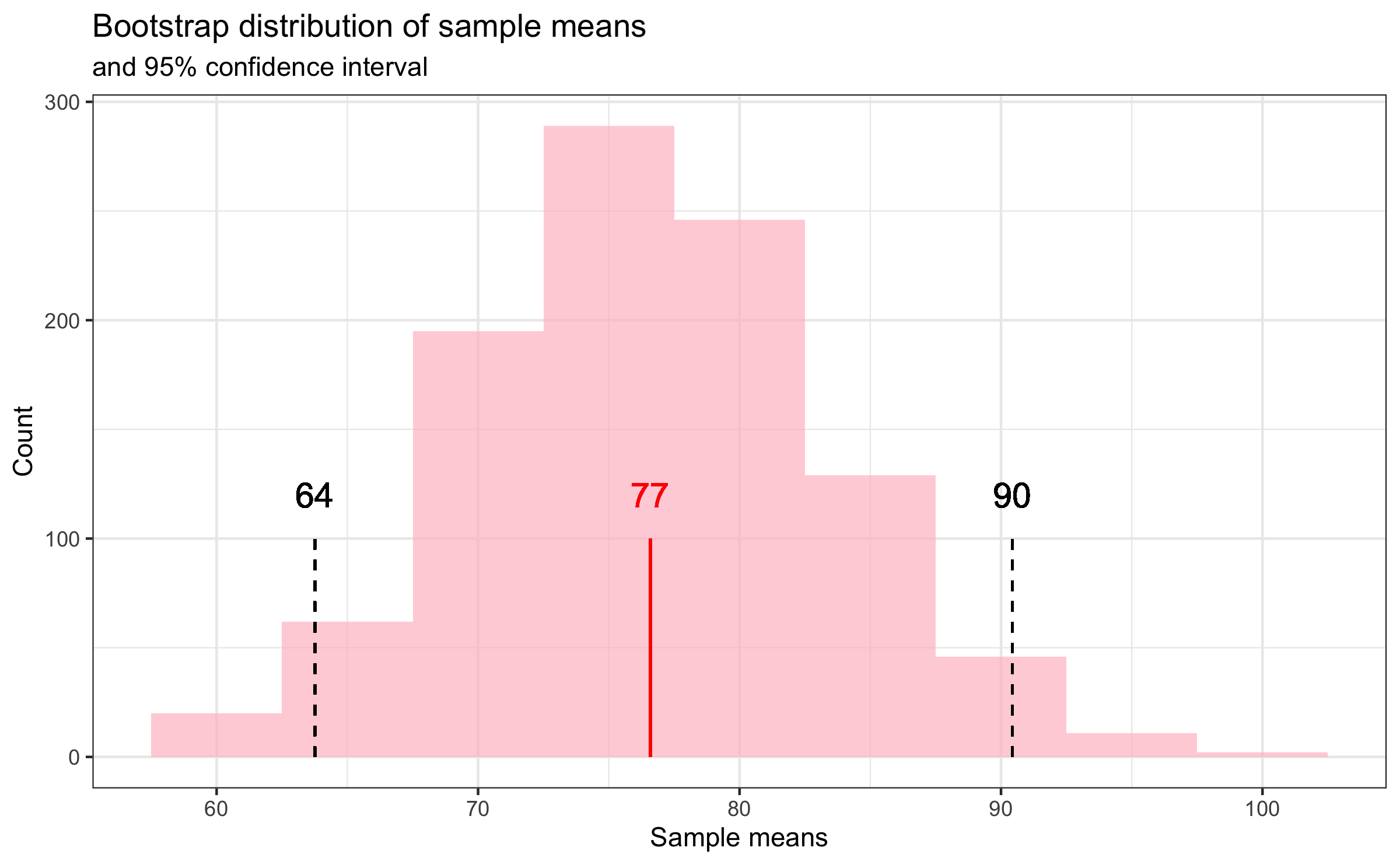
Step 4
Calculate the bounds of the bootstrap interval by using percentiles of the bootstrap distribution.
 The 95% confidence interval for the mean price per guest per night
among Airbnb rentals with at least ten reviews in Asheville is ($64, $90).
The 95% confidence interval for the mean price per guest per night
among Airbnb rentals with at least ten reviews in Asheville is ($64, $90).
Bulletin
Watch videos for Prepare: June 1
Mid-course feedback on Sakai due Fridy, June 3 at 11:59pm
Kick-off of the final project! Read intructions carefully
Project proposal due Friday, June 3 at 11:59pm
Lab 04 due tonight at 11:59pm