Central Limit Theorem 1
Bora Jin
Material
🎥 Watch Central Limit Theorem
Optional: 📖 Read IMS: Chapter 13 - Inference With Mathematical Models
Today's Goal
- Use Central Limit Theorem to define distribution of sample means
- Calculate probabilities from the normal distribution
Quantifying Variability
We can quantify the variability of sample statistics using different approaches:
- Simulation: via bootstrapping or "resampling" techniques
or
- Theory: via the Central Limit Theorem
Quantifying Variability
We can quantify the variability of sample statistics using different approaches:
- Simulation: via bootstrapping or "resampling" techniques
or
- Theory: via the Central Limit Theorem
Today we will focus on Theory.
Quiz
Q - What is a sampling distribution of the sample mean?
From one random sample of size n, calculate the sample mean ¯X1
Quiz
Q - What is a sampling distribution of the sample mean?
From one random sample of size n, calculate the sample mean ¯X1
From a second random sample of size n, calculate the sample mean ¯X2
Quiz
Q - What is a sampling distribution of the sample mean?
From one random sample of size n, calculate the sample mean ¯X1
From a second random sample of size n, calculate the sample mean ¯X2
⋮
Repeat this many times.
Quiz
Q - What is a sampling distribution of the sample mean?
From one random sample of size n, calculate the sample mean ¯X1
From a second random sample of size n, calculate the sample mean ¯X2
⋮
Repeat this many times.
We call the distribution of ¯X the sampling distribution.
Quiz
Q - Apply the central limit theorem (CLT) on sample means.
Let a random variable X have a mean μ and standard deviation σ. Then the sampling distribution of the sample mean ¯X=X1+X2+⋯+Xnn
Quiz
Q - Apply the central limit theorem (CLT) on sample means.
Let a random variable X have a mean μ and standard deviation σ. Then the sampling distribution of the sample mean ¯X=X1+X2+⋯+Xnn
- Has the mean μ
Quiz
Q - Apply the central limit theorem (CLT) on sample means.
Let a random variable X have a mean μ and standard deviation σ. Then the sampling distribution of the sample mean ¯X=X1+X2+⋯+Xnn
Has the mean μ
Has the standard error σ/√n
standard error of a sample mean = standard deviation of its sampling distribution or an estimate of that standard deviation
Quiz
Q - Apply the central limit theorem (CLT) on sample means.
Let a random variable X have a mean μ and standard deviation σ. Then the sampling distribution of the sample mean ¯X=X1+X2+⋯+Xnn
Has the mean μ
Has the standard error σ/√n
standard error of a sample mean = standard deviation of its sampling distribution or an estimate of that standard deviation
- If the sample size n is large enough, the sampling distribution of ¯X is approximately normally distributed.
As n→∞, ¯X converges in distribution to N(μ,σ/√n).
Quiz
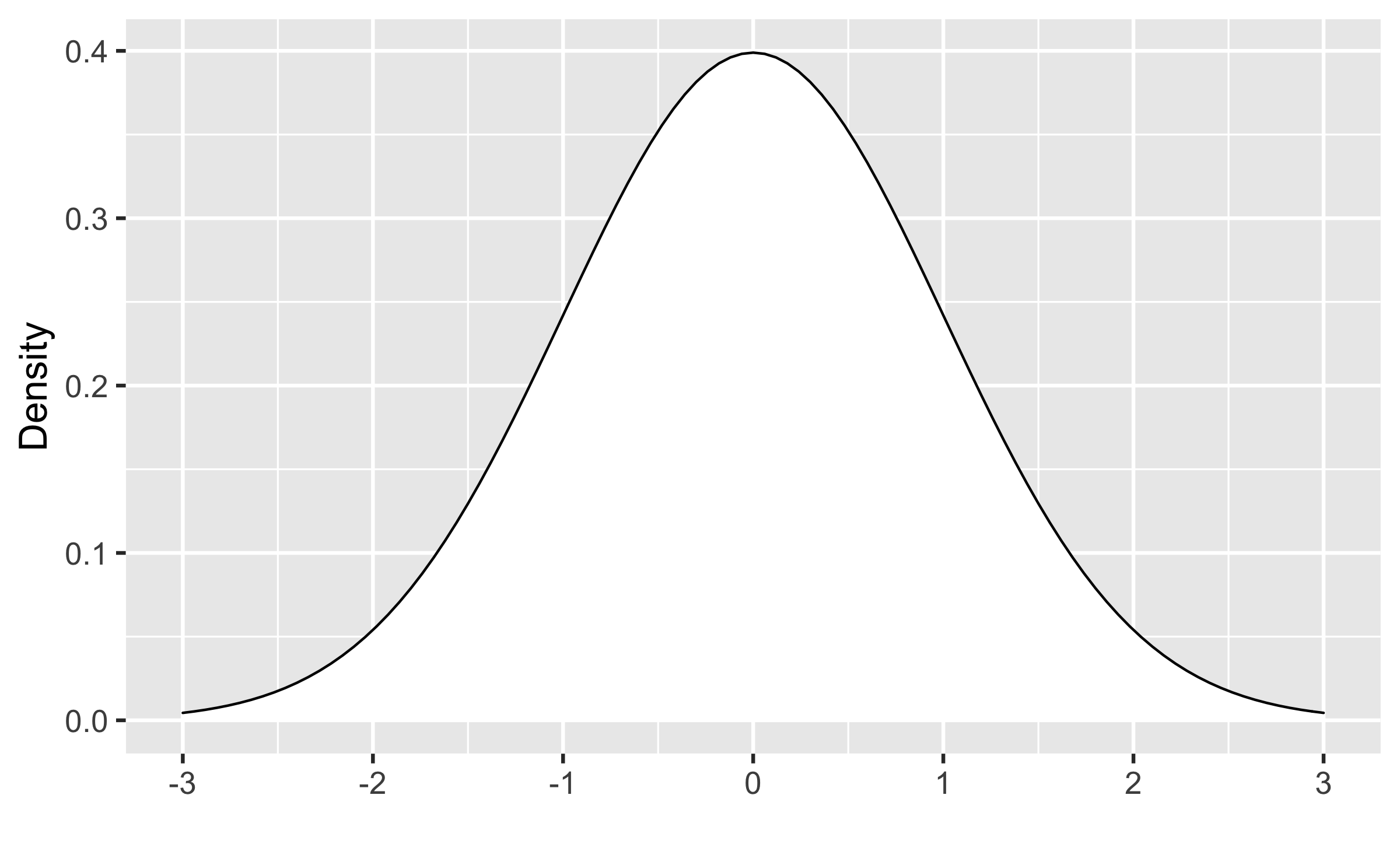
Q - Describe density of a normal distribution.
- unimodal (peak at μ)
- symmetric around μ
- bell-shaped
Quiz
Q - The CLT holds only if X∼N(μ,σ). (T/F)
F
X can be from any distribution with a mean μ and standard deviation σ.
Let's play with weird looking original distributions - Click!
Quiz
Q - What are the two conditions for CLT to hold?
Independence
- {X1,⋯,Xn} must be independent to one another
- One observation's value should not "influence" another observation's value.
- Rules of thumb to check independence:
- Completely random sampling
- If taken without replacement, n should be less than 10% of the population size
Quiz
Q - What are the two conditions for CLT to hold?
Sample size n / distribution
- If X is numerical, n>30
- If X is categorical, at least 10 successes and 10 failures
- If X∼N(μ,σ), then the distribution of sample means will also be exactly normal, regardless of the sample size.
Recap
- If certain assumptions are satisfied, regardless of the shape of the population distribution, the sampling distribution of the mean follows an approximately normal distribution.
Recap
If certain assumptions are satisfied, regardless of the shape of the population distribution, the sampling distribution of the mean follows an approximately normal distribution.
The center of the sampling distribution is at the center of the population distribution.
Recap
If certain assumptions are satisfied, regardless of the shape of the population distribution, the sampling distribution of the mean follows an approximately normal distribution.
The center of the sampling distribution is at the center of the population distribution.
The sampling distribution is less variable than the population distribution by a factor of 1/√n.
Recap
If certain assumptions are satisfied, regardless of the shape of the population distribution, the sampling distribution of the mean follows an approximately normal distribution.
The center of the sampling distribution is at the center of the population distribution.
The sampling distribution is less variable than the population distribution by a factor of 1/√n.
As n increases, the standard error (the spread of the sampling distribution) decreases.
Quiz
Q - What is an appropriate code to calculate P(Z<1.2) where Z∼N(0,1)?
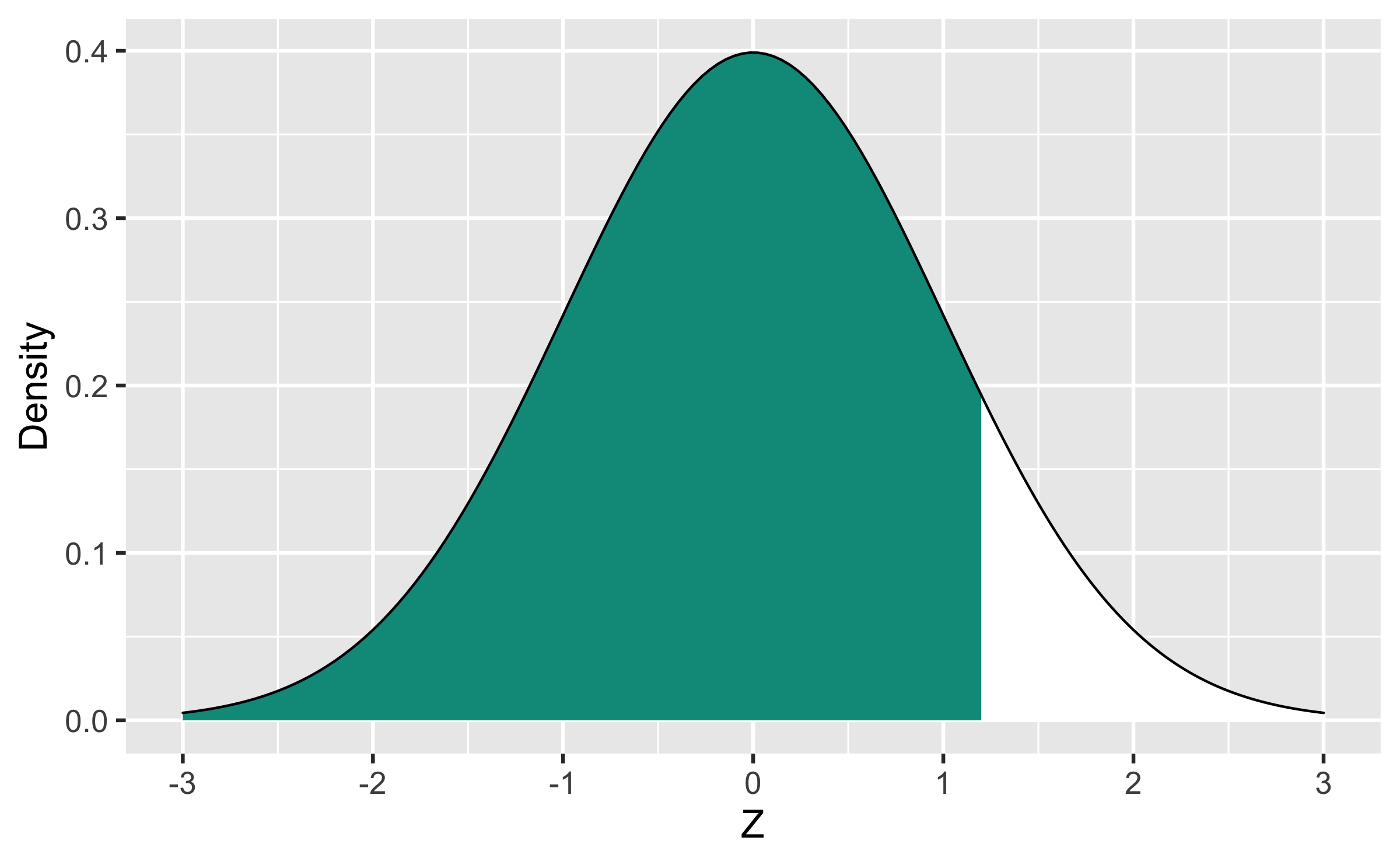
pnorm(1.2)## [1] 0.8849303Quiz
Q - What is an appropriate code to calculate P(−2<X<7) where X∼N(1,3)?
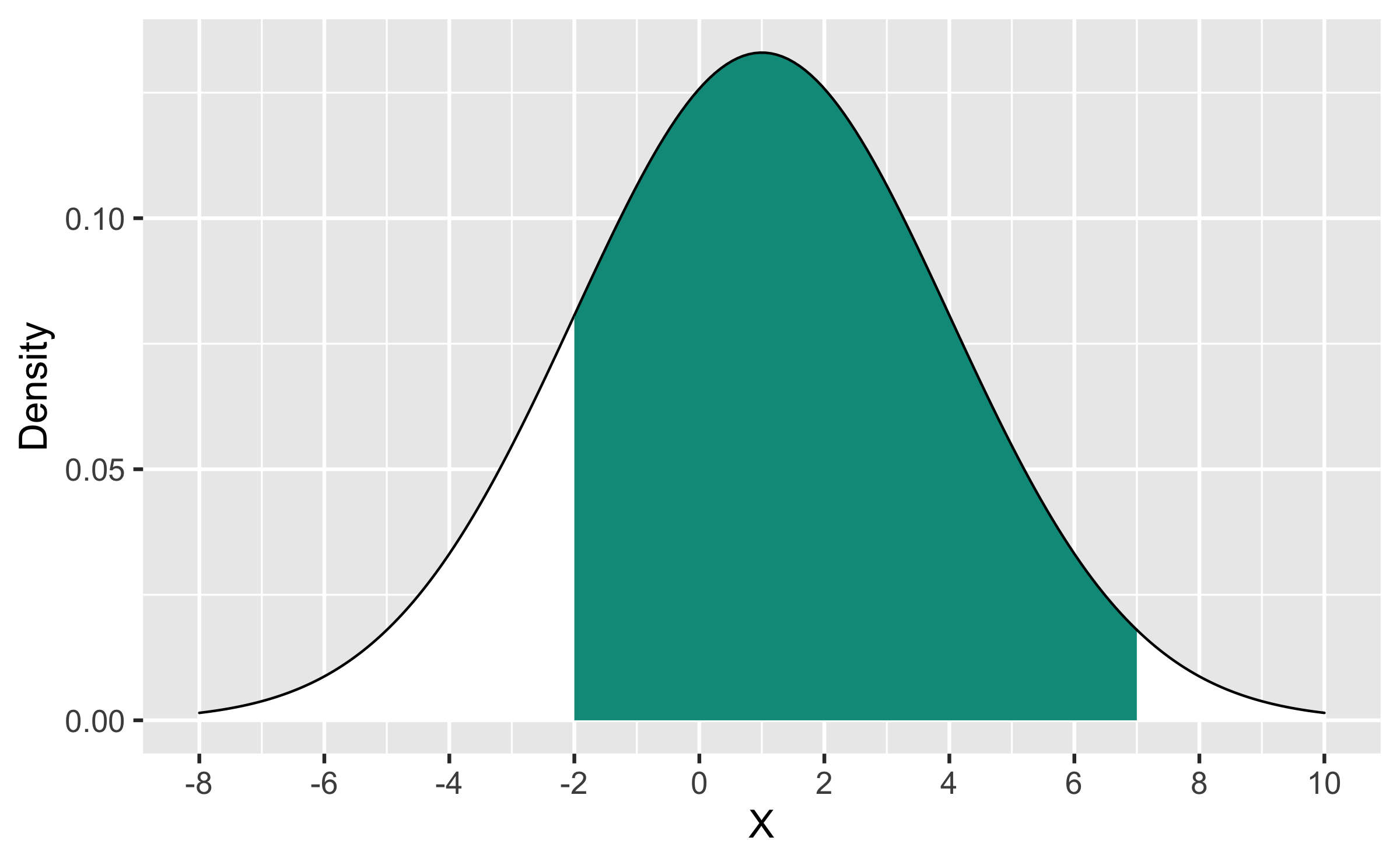
pnorm(7, mean = 1, sd = 3) - pnorm(-2, mean = 1, sd = 3)## [1] 0.8185946Quiz
Q - What is an appropriate code to find q s.t. P(X>q)=0.05 where X∼N(−1,2)?
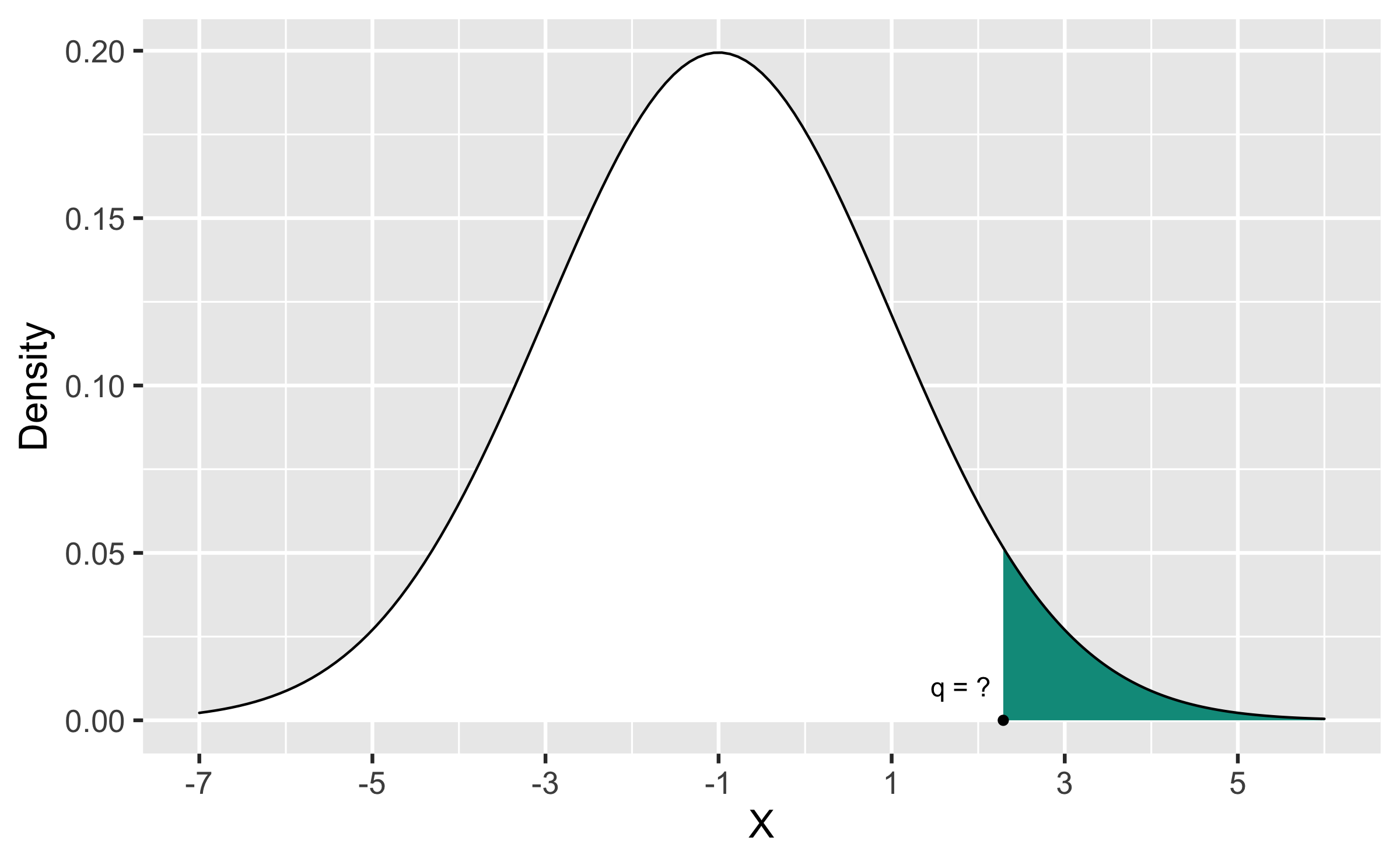
Quiz
Q - What is an appropriate code to find q s.t. P(X>q)=0.05 where X∼N(−1,2)?

qnorm(0.05, mean = -1, sd = 2, lower.tail = FALSE)## [1] 2.289707Bulletin
Watch videos for Prepare: June 7
Project proposal feedback released
Lab06 due Tuesday, June 7 at 11:59pm
HW03 due Wednesday, June 8 at 11:59pm
Submit
ae17