Central Limit Theorem 2

class: center, middle, inverse, title-slide

# Central Limit Theorem 2
### Bora Jin

---

layout: true
  
<div class="my-footer">
<span>
<a href="https://introds.org" target="_blank">introds.org</a>
</span>
</div>

---

## Material

🎥 Watch [Inference Using Central Limit Theorem](https://warpwire.duke.edu/w/WQ4GAA/)

- [Slides](https://sta199-fa21-003.netlify.app/slides/clt-inference.html#1)

Optional: 📖 Read

- [IMS: Section 16.2 - Mathematical Model for a Proportion](https://openintro-ims.netlify.app/inference-one-prop.html#one-prop-norm)
- [IMS: Section 17.3 - Mathematical Model for Difference in Proportions](https://openintro-ims.netlify.app/inference-two-props.html#math-2prop)
- [IMS: Section 19.2 - Mathematical Model for a Mean](https://openintro-ims.netlify.app/inference-one-mean.html#one-mean-math)
- [IMS: Section 20.3 - Mathematical Model for Testing Difference in Means](https://openintro-ims.netlify.app/inference-two-means.html#math2samp)

---

## Today's Goal

- Use Central Limit Theorem (CLT) to conduct inference on a population mean
- Conduct CLT-based inference step-by-step and using the `infer` package
- Understand t-distribution vs. standard normal, N(0,1) distribution

---

## Quiz

**Q - State the central limit theorem.**

For a population with a well-defined mean `$\mu$` and standard deviation `$\sigma$`,
these three properties hold for the distribution of sample average `$\bar{X}$`,
assuming certain conditions hold:

✅ The distribution of the sample statistic is

--
**approximately** normal

✅ The distribution is centered at

--
the population parameter (often interest of inference)

✅ The variability of the distribution is **inversely** proportional to the square root of

--
the sample size

---

## Quiz

**Q - Why do we care about the distribution of sample mean?**

We can estimate / test for a population mean.

We can construct a confidence interval or conduct a hypothesis test for the population mean using the CLT-based distribution in place of a simulation-based distribution of sample mean.

---

## Quiz

**Q - What is the distribution of sample mean by CLT?**

When the population mean `$\mu$` and the population standard deviation `$\sigma$` are known,

`$$\bar{X} \sim N(\mu, \sigma/\sqrt{n}) \Leftrightarrow Z = \frac{\bar{X}-\mu}{\sigma/\sqrt{n}} \sim N(0,1)$$`

approximately, for a large enough `$n$`.

- N(0,1) is standard normal distribution.
- Often, a random variable following the standard normal distribution is denoted by `$Z$`.

---

## Quiz

**Q - What if** `$\sigma$` **is unknown?**

- We approximate `$\sigma$` with the sample standard deviation.

`$$Z = \frac{\bar{X}-\mu}{\sigma/\sqrt{n}} \rightarrow T = \frac{\bar{X}-\mu}{S/\sqrt{n}}$$`
where `$S^2 = \sum_{i=1}^n(X_i - \bar{X})^2/(n-1)$`
--

- `$\sigma$` replaced by `$S$`! (The realized value of `$S$` from a sample is `$s$`.)
--

- This change renders the random variable `$T$` follow another distribution than the standard normal distribution, i.e., `$$T \sim t_{n-1}$$`
where `$t_{n-1}$` is a t-distribution with `$n-1$` degrees of freedom.

---

## Quiz

**Q - List properties of the t-distribution.**

- Its shape is

--
unimodal, symmetric, centered at 0 similarly to N(0,1).

- Its tails are

--
thicker than N(0,1).

- It is fully defined by

--
the degrees of freedom.

---

## Quiz

**Q - Black solid line is N(0,1). What is the t-distribution with df = 1, 3, 10, and 30?**

---

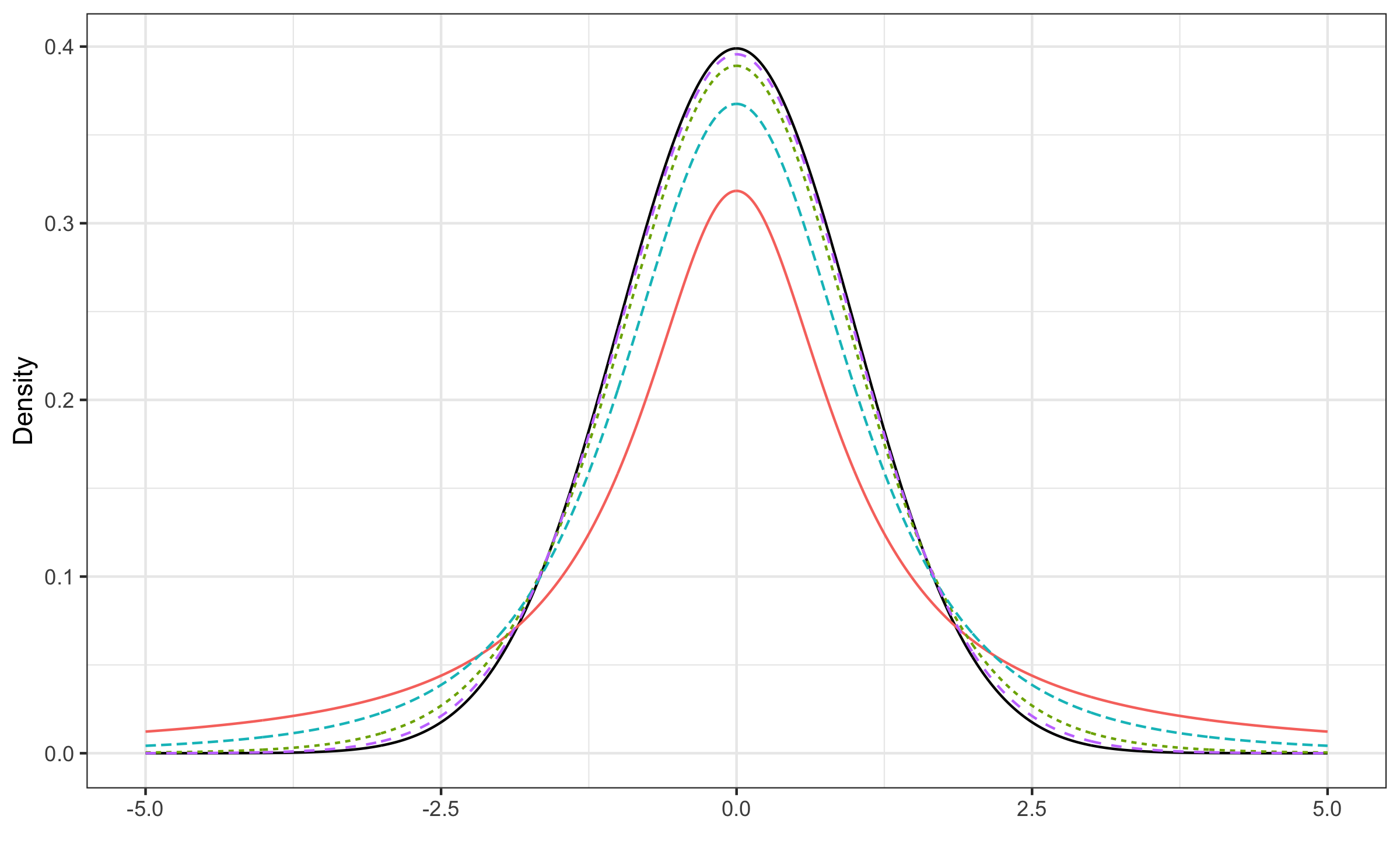
## Quiz

**Q - Black solid line is N(0,1). What is the t-distribution with df = 1, 3, 10, and 30?**

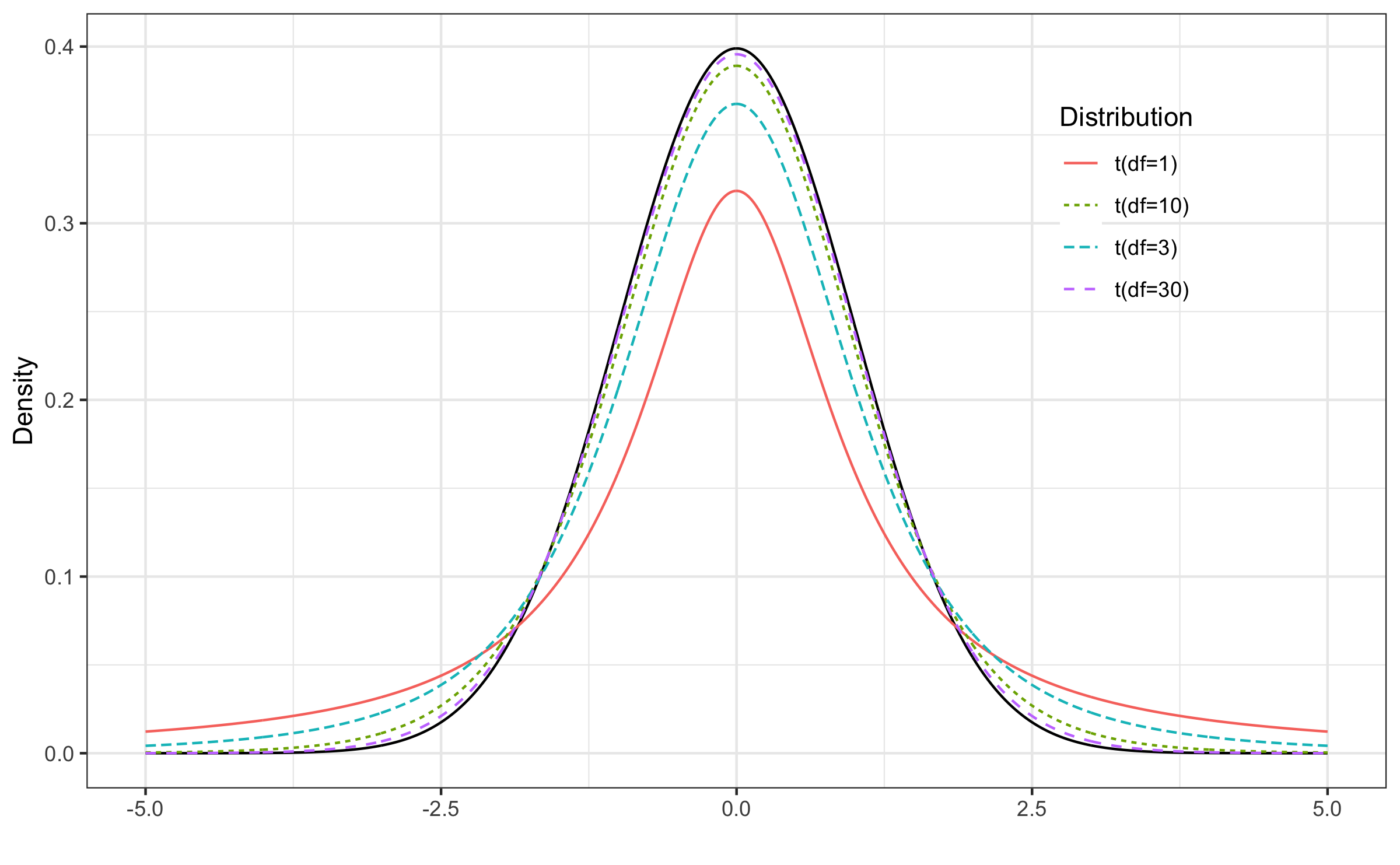
<img src="18-clt2_BJ_files/figure-html/unnamed-chunk-3-1.png" width="55%" style="display: block; margin: auto;" />
- thicker tails 
- As the degrees of freedom increases, the t-distribution becomes more like N(0,1)

---

## Quiz

**Q - What is an appropriate code to calculate** `$P(T < 1.2)$` **where** `$T \sim t_5$`**?**

<img src="18-clt2_BJ_files/figure-html/unnamed-chunk-4-1.png" width="50%" style="display: block; margin: auto;" />
--

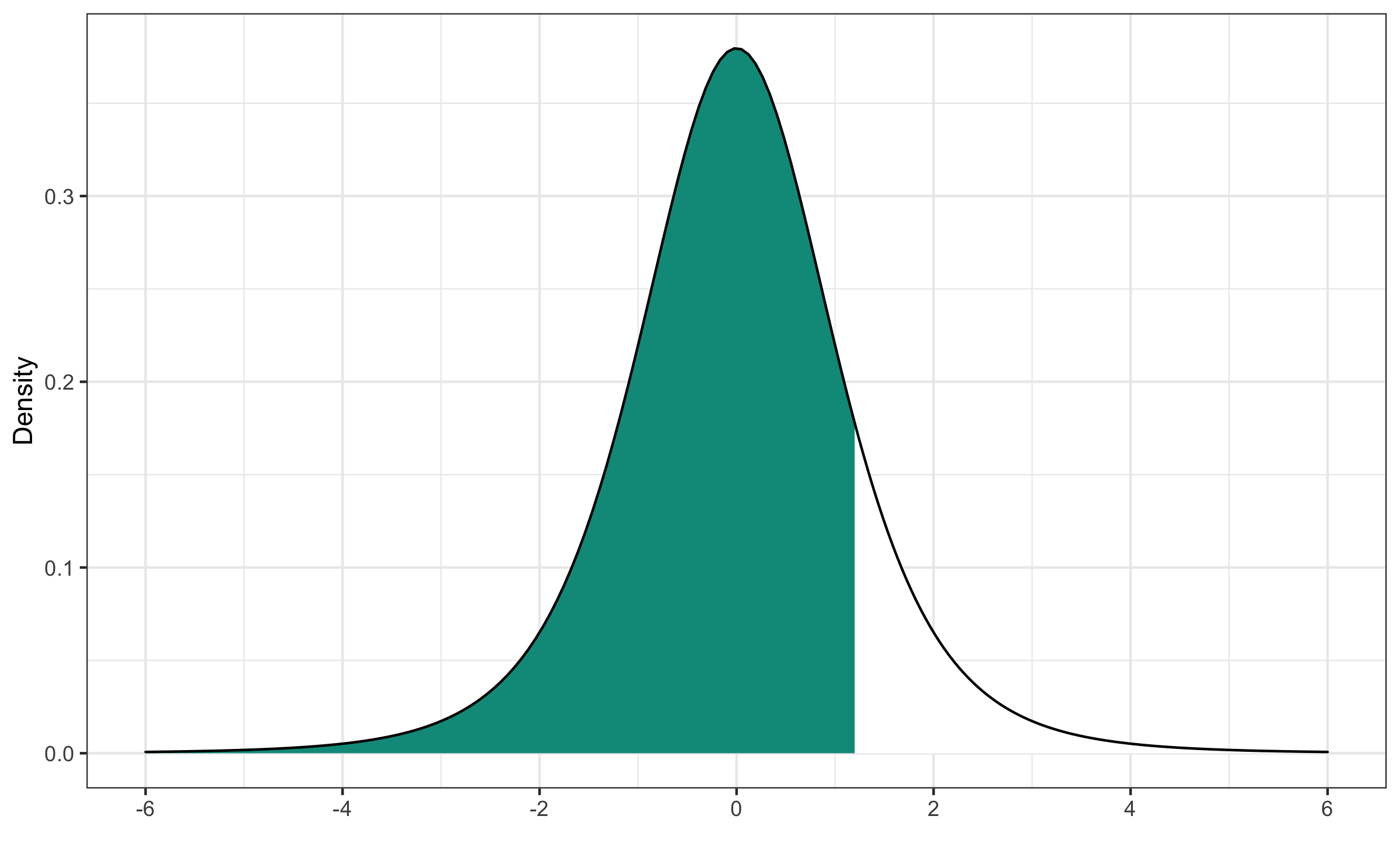
```r
pt(1.2, df = 5)
```

```
## [1] 0.8580545
```

---

## Quiz

**Q - What is an appropriate code to calculate** `$P(-2 < T < 3)$` **where** `$T \sim t_{10}$`**?**

<img src="18-clt2_BJ_files/figure-html/unnamed-chunk-6-1.png" width="50%" style="display: block; margin: auto;" />
--

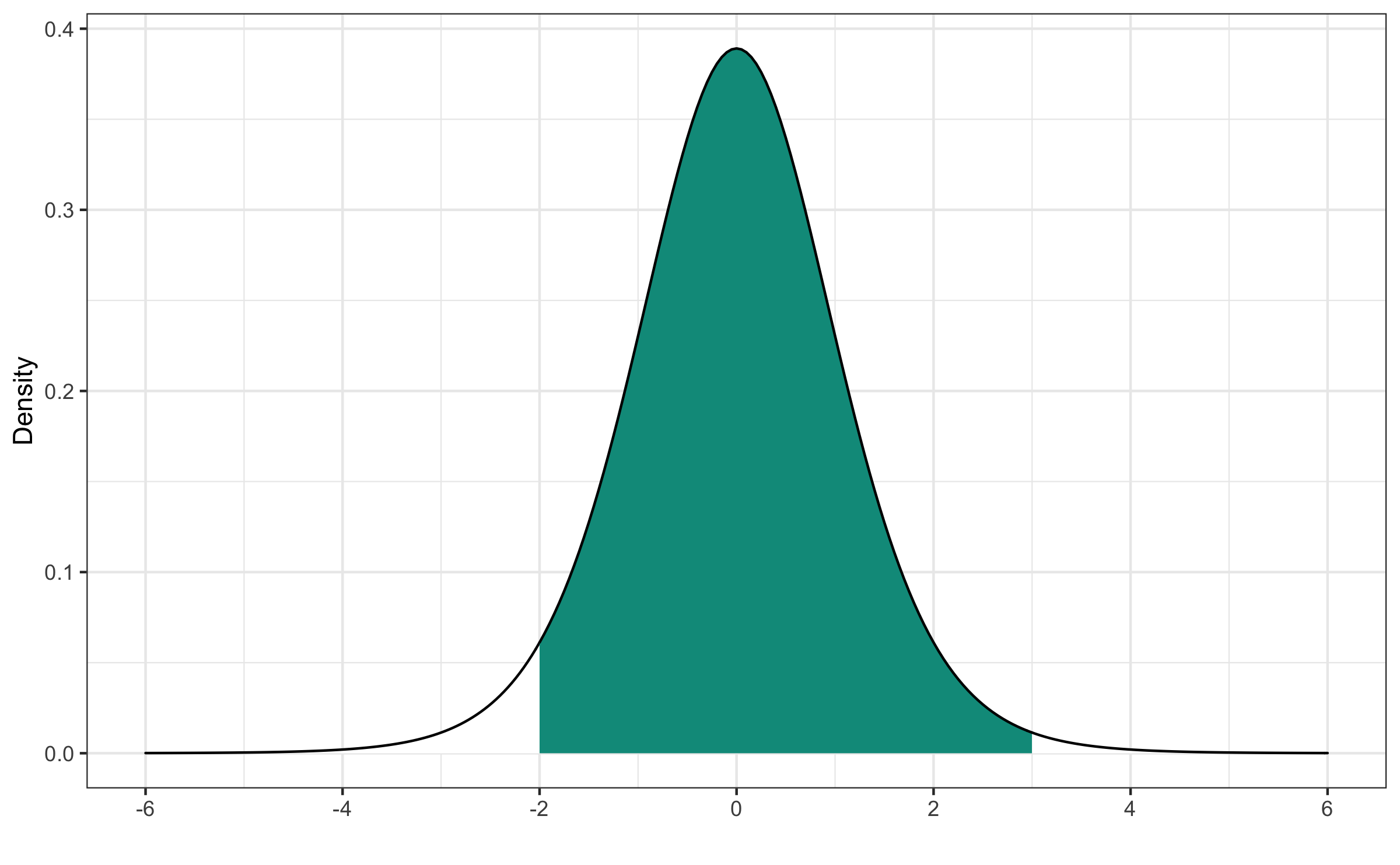
```r
pt(3, df = 10) - pt(-2, df = 10)
```

```
## [1] 0.9566342
```

---

## Quiz

**Q - What is an appropriate code to find** q **s.t.** `$P(T > q) = 0.25$` **where** `$X \sim t_7$`**?**

<img src="18-clt2_BJ_files/figure-html/unnamed-chunk-8-1.png" width="50%" style="display: block; margin: auto;" />
--

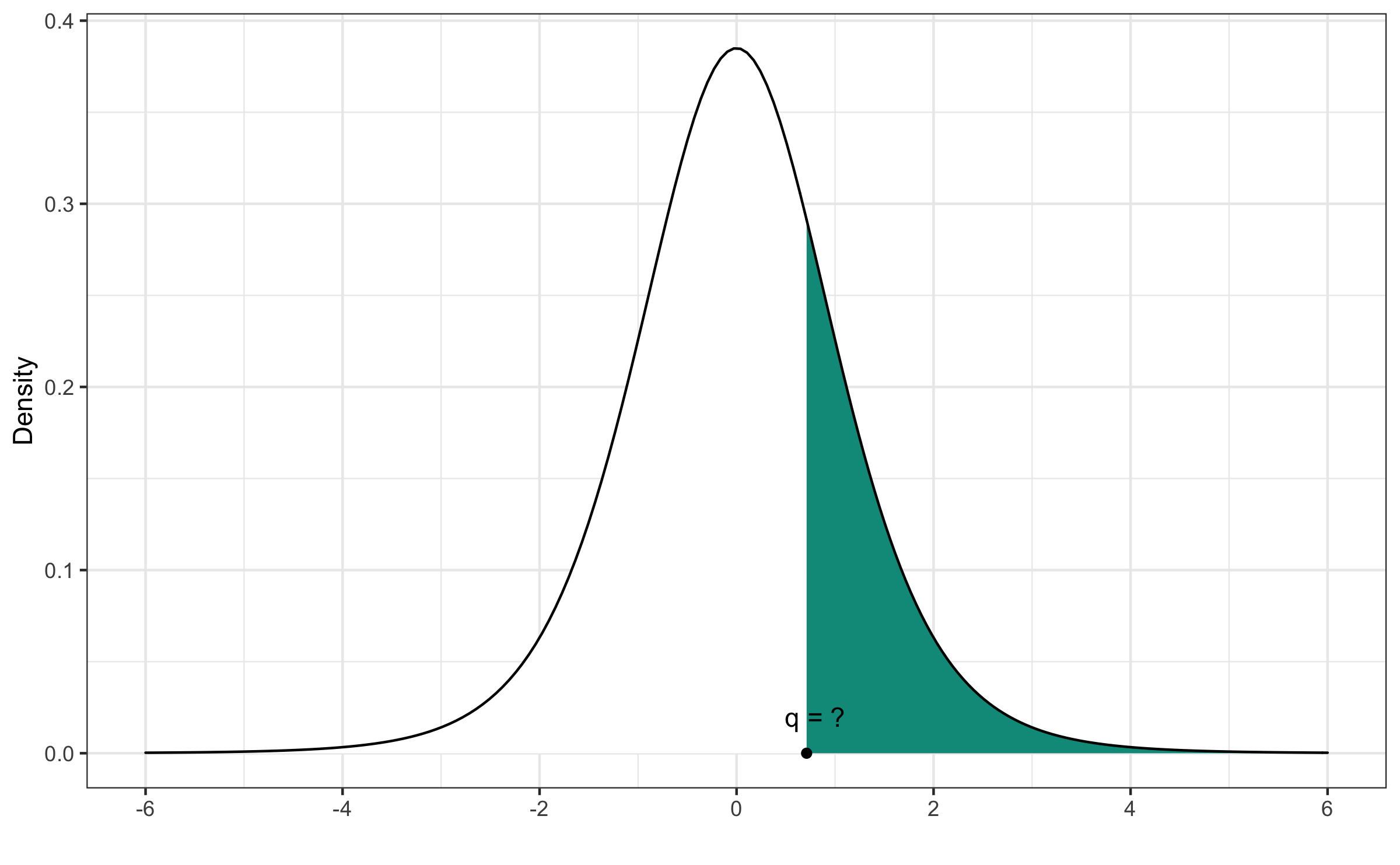
```r
qt(0.25, df = 7, lower.tail = FALSE)
```

```
## [1] 0.7111418
```

---

## Quiz: HT

Let's conduct a hypothesis test for `$H_0: \mu = 5$` vs. `$H_1: \mu \neq 5$`. 
We don't know the population standard deviation. We have a random sample of size 100. 
The CLT conditions are checked.

**Q - What is the test statistic and its null distribution by CLT?**

- The test statistic is calculated by `$t = \frac{\bar{x} - 5}{s/10}$`.

- Under the null, 
`$$T = \frac{\bar{X} - 5}{S/10} \sim t_{99}$$`
- Capital letters for random variables and lowercase letters for observed values

---

## Quiz: HT

**Q - What does it mean that the test statistic is 3.5?**

The observed sample mean `$\bar{x}$` is 3.5 standard errors above the hypothesized population mean, 5.

---

## Quiz: CI

**Q - What is the formula to obtain a** `$1-\alpha$` **confidence interval for** `$\mu$` **?**

`$$\bar{x} \pm t^*_{n-1}\times \frac{s}{\sqrt{n}}$$`

where `$t^*_{n-1}$` is a critical value that satisfies `$P(T > t^*_{n-1}) = \alpha/2$` for `$T \sim t_{n-1}$`.

**Q - What is the R function to calculate** `$t^*_{n-1}$`?

```r
qt(alpha/2, df = n-1, lower.tail = FALSE)
```

---

## Quiz

**Q - What is the function in the** `infer` **package to use for CLT-based inference when** `$\sigma$` **is unknown?**

`t_test()`

---

class: middle, center

# Questions?

---

## Let's Practice Together!

Go to [AE 18: Central Limit Theorem 2](https://sta199-summer22.netlify.app/appex/ae18_BJ.html)

---

## Bulletin

- Tomorrow is Ask-for-Help day. Bring your questions.

- Lab06 due tonight at 11:59pm

- HW03 due Wednesday, June 8 at 11:59pm

- Tomorrow (June 8) is the last day to withdraw with W

- Submit `ae18`