Introduction to Linear Models
Bora Jin
Today's Goal
- Understand the language and notation of linear modeling
- Use
tidymodelsandstatpackage to make inference under a linear regression model
Quiz
Q - What do we need models for?
- Explain the relationship between variables
- Make predictions (e.g., Amazon / Netflix recommendations)
- We will focus on linear models (straight lines!) but there are many other types.
Quiz
Q - What is a predicted value?
- Output of a model function
- Typical or expected value of the response variable conditioning on the explanatory variable
- ^y=f(x)
Quiz
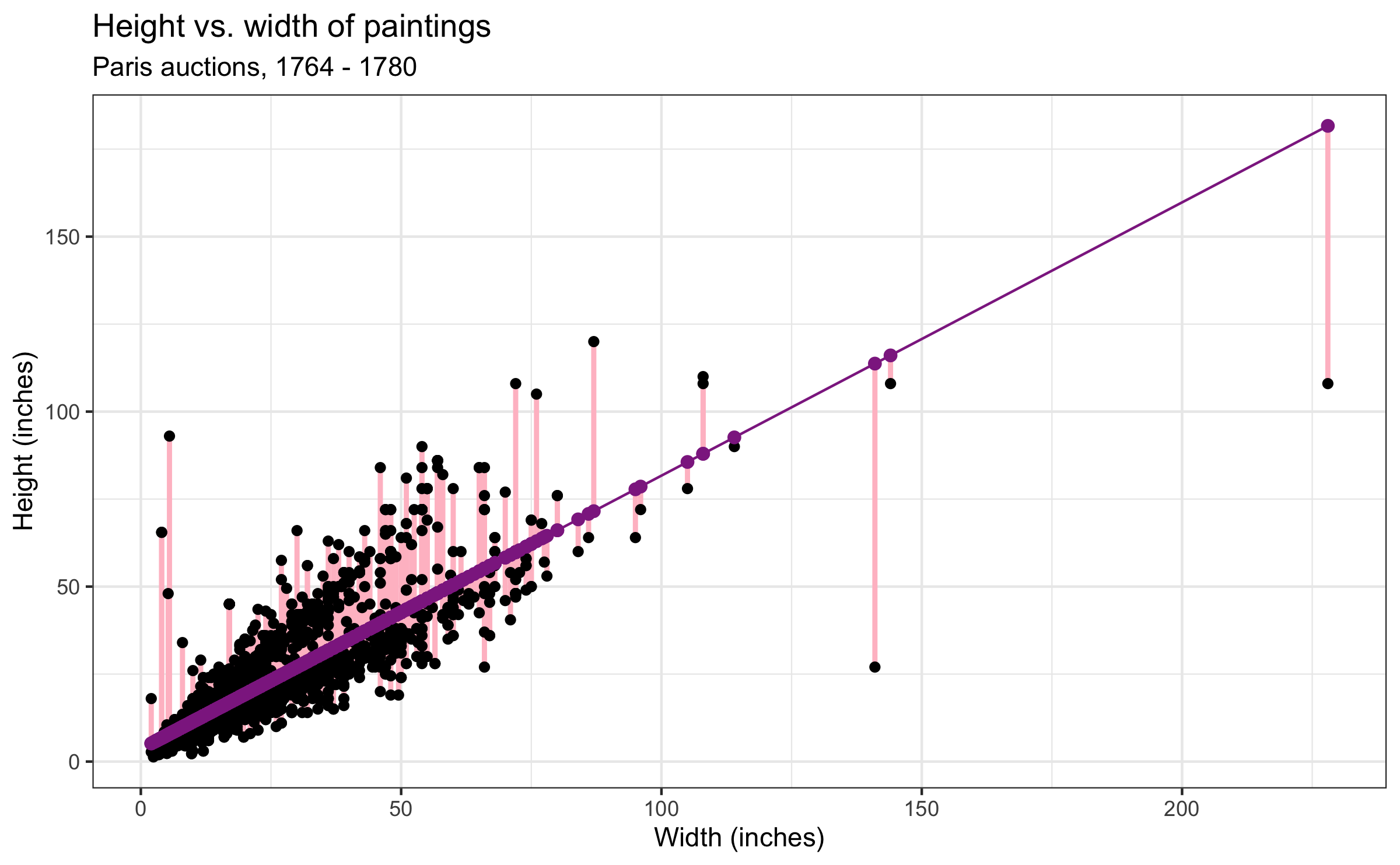
Q - What is a residual?
- A measure of how far each observation is from its predicted value
- residual = observed value - predicted value
- e=y−^y
Quiz
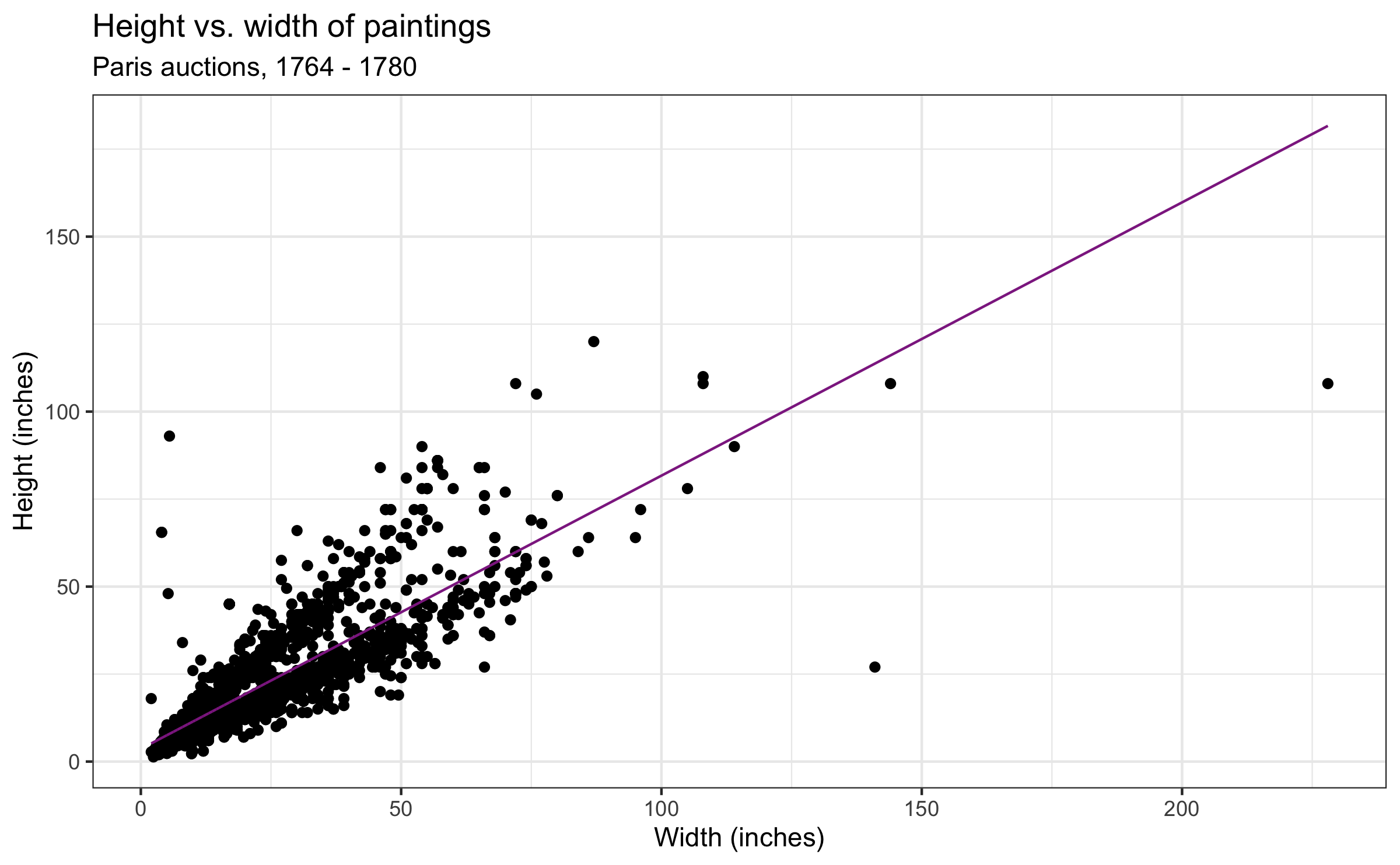
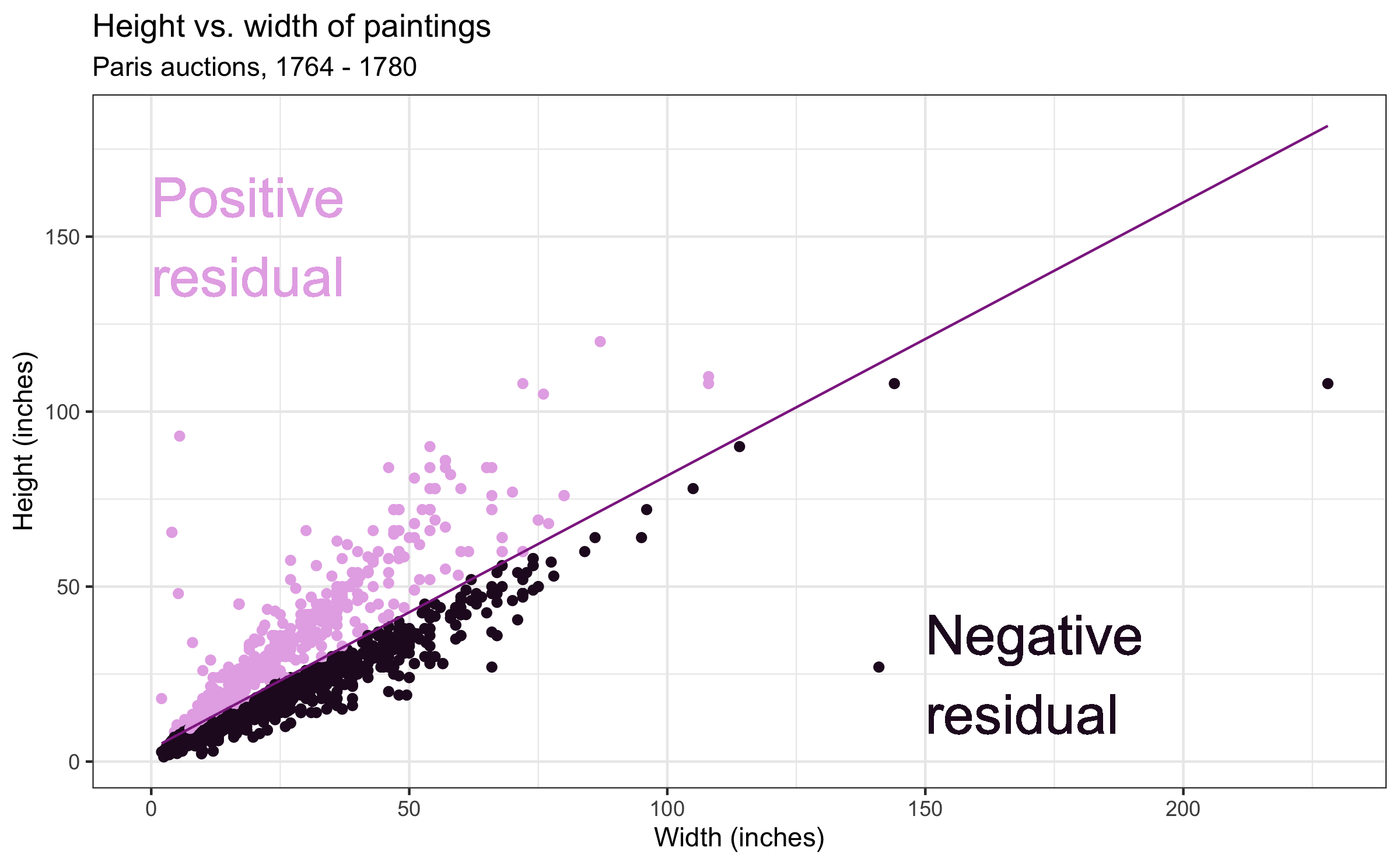
Q - What is a residual?
- Where are the paintings with positive / negative residual relative to the fitted line?
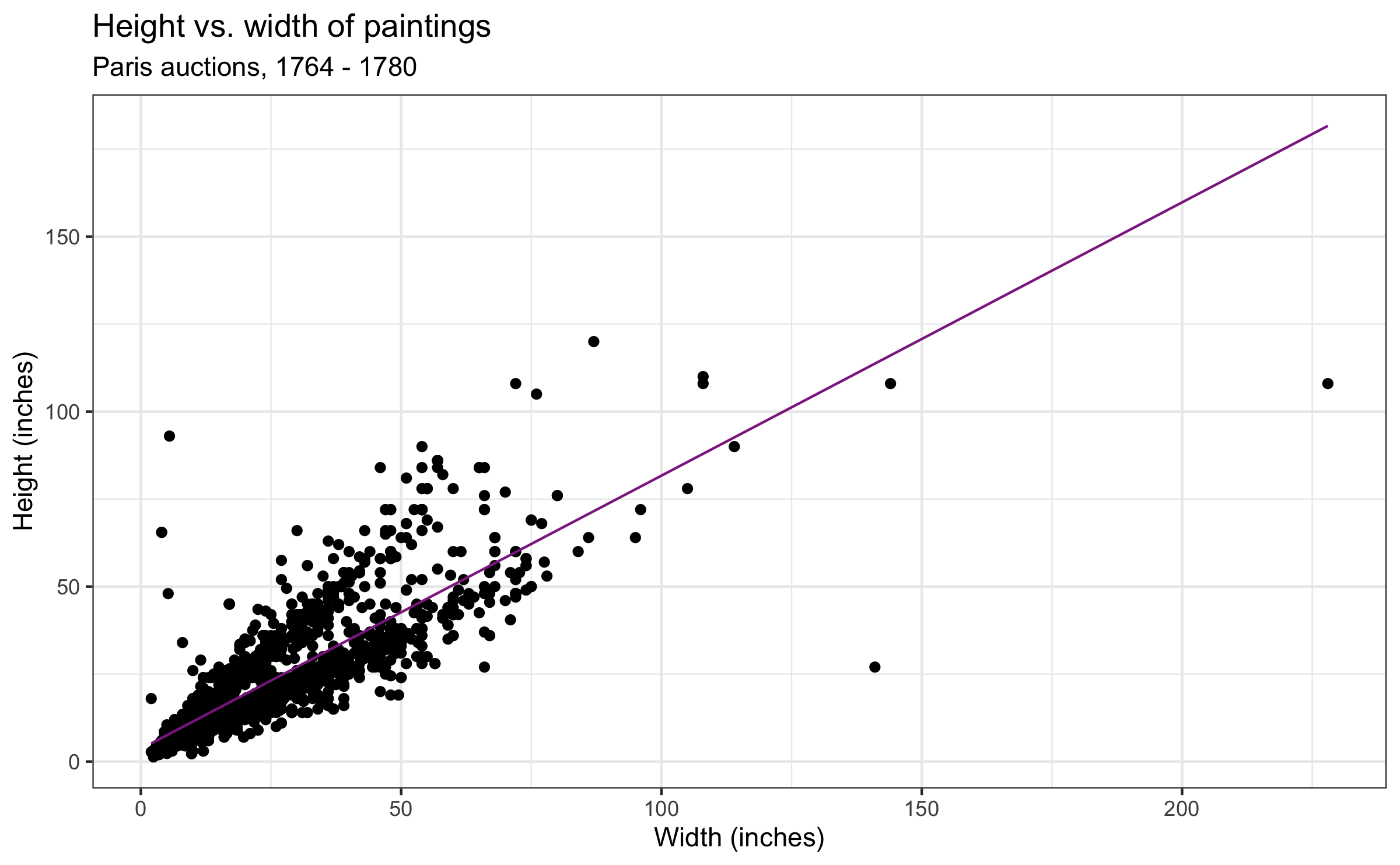
Quiz
Q - What is a residual?
- Where are the paintings with positive / negative residual relative to the fitted line?
Quiz
Q - What is a residual?
- Where are the paintings with positive / negative residual relative to the fitted line?

- What does a negative residual mean?
Quiz
Q - What is a residual?
- Where are the paintings with positive / negative residual relative to the fitted line?

- What does a negative residual mean? The predicted value is greater than the actual value.
Quiz
Q - What are some upsides and downsides of models?
Upsides:
- Can sometimes reveal patterns that are not evident in visualizations.
Quiz
Q - What are some upsides and downsides of models?
Upsides:
- Can sometimes reveal patterns that are not evident in visualizations.
Downsides:
- Might impose structures that are not really there.
- Be skeptical about modeling assumptions!
Quiz
Q - Models always entail uncertainty. Which part of the following visualization and table is relevant to uncertainty?
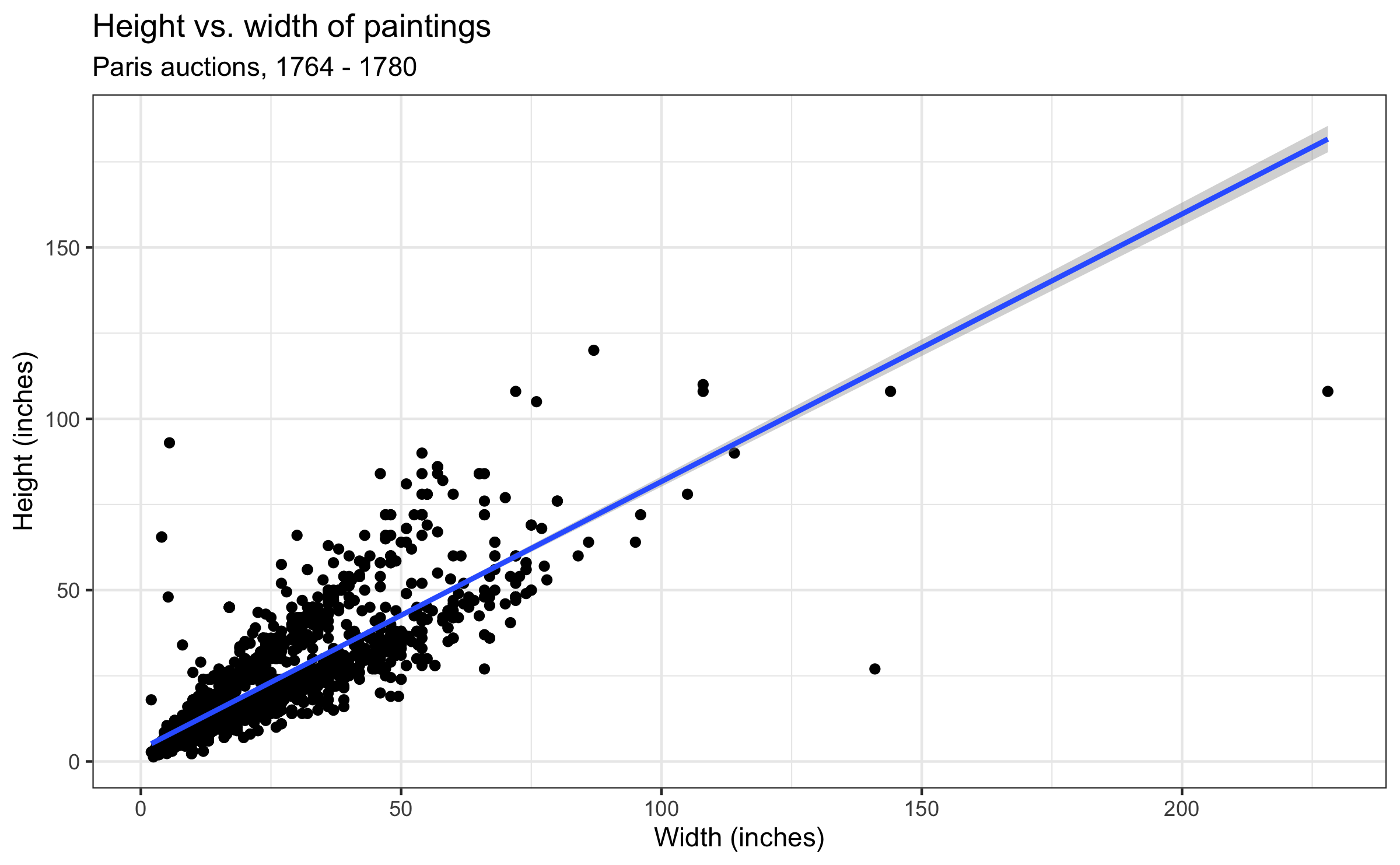
## # A tibble: 2 × 3## term estimate std.error## <chr> <dbl> <dbl>## 1 (Intercept) 3.62 0.254 ## 2 Width_in 0.781 0.00950Quiz
Q - Models always entail uncertainty. Which part of the following visualization and table is relevant to uncertainty?

## # A tibble: 2 × 3## term estimate std.error## <chr> <dbl> <dbl>## 1 (Intercept) 3.62 0.254 ## 2 Width_in 0.781 0.00950- Uncertainty is as important as the fitted line, if not more.
Linear Model with a Single Predictor
We are interested in β0 and β1 in the following model:
yi=β0+β1xi+ϵi
- yi: response variable value for the ith observation
- β0: population parameter for the intercept
- β1: population parameter for the slope
- xi: independent variable (or predictor, covariate) value for the ith observation
- can be numeric or categorical
- ϵi: random error for the ith observation
Linear Model with a Single Predictor
As usual, we have to estimate the true parameters with sample statistics:
^yi=^β0+^β1xi
- ^yi: predicted value for the ith observation
- ^β0: estimate for β0
- ^β1: estimate for β1
Least Squares Regression
In the least squares regression the estimates are calculated in a way to minimize the sum of squared residuals. In other words, if I have n observations and the ith residual is ei=yi−^yi, then the fitted regression line minimizes ∑ni=1e2i.
Q - Why do we minimize the "squares" of the residuals?
Least Squares Regression
In the least squares regression the estimates are calculated in a way to minimize the sum of squared residuals. In other words, if I have n observations and the ith residual is ei=yi−^yi, then the fitted regression line minimizes ∑ni=1e2i.
Q - Why do we minimize the "squares" of the residuals?
- Some residuals are positive, and others are negative. If we just naively sum them, they will cancel each other.
- Residuals are not good in both directions. We especially want to penalize residuals that are large in absolute magnitude.
Least Squares Regression
In the least squares regression the estimates are calculated in a way to minimize the sum of squared residuals. In other words, if I have n observations and the ith residual is ei=yi−^yi, then the fitted regression line minimizes ∑ni=1e2i.
Q - Why do we minimize the "squares" of the residuals?
- Some residuals are positive, and others are negative. If we just naively sum them, they will cancel each other.
- Residuals are not good in both directions. We especially want to penalize residuals that are large in absolute magnitude.
Click to play with least squares regression!
Quiz
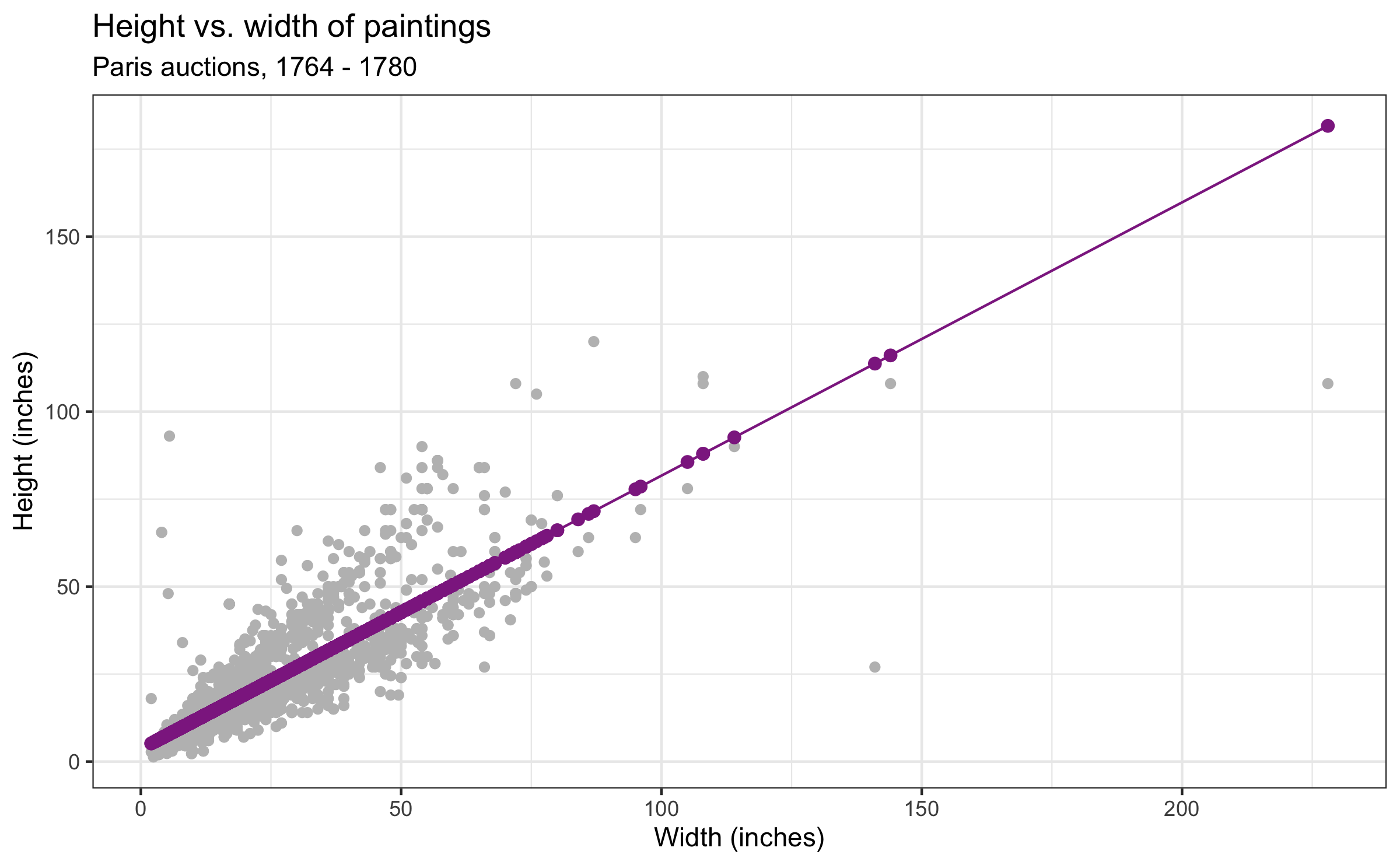
Q - What are some properties of the least squares regression?
- The fitted line always goes through (¯x,¯y)
¯y=^β0+^β1¯x
- The fitted line has a positive slope ( ^β1 > 0) if x and y are positively correlated and a negative slope if they are negatively correlated. The line has 0 slope if they are not correlated.
- The sum of the residuals is always zero: ∑ni=1ei=0.
- The residuals and x values are uncorrelated.
Quiz
Q - Based on the code and output below, write a model formula with parameter estimates.
linear_reg() %>% set_engine("lm") %>% fit(Height_in ~ Width_in, data = pp) %>% tidy()## # A tibble: 2 × 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 3.62 0.254 14.3 8.82e-45## 2 Width_in 0.781 0.00950 82.1 0Quiz
Q - Based on the code and output below, write a model formula with parameter estimates.
linear_reg() %>% set_engine("lm") %>% fit(Height_in ~ Width_in, data = pp) %>% tidy()## # A tibble: 2 × 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 3.62 0.254 14.3 8.82e-45## 2 Width_in 0.781 0.00950 82.1 0ˆheighti=3.62+0.781×widthi
Quiz
Q - Interpret slope and intercept estimates in the context of data.
ˆheighti=3.62+0.781×widthi
Quiz
Q - Interpret slope and intercept estimates in the context of data.
ˆheighti=3.62+0.781×widthi
- Slope: For each additional inch the painting is wider, the height is expected to be higher, on average, by 0.781 inches.
- Always remember, the slope is about correlation, not causation. We are not saying increasing one inch in width of a painting will cause it to become 0.781 inches taller.
- Intercept: Paintings that are 0 inches wide are expected to be 3.62 inches high, on average.
Quiz
Q - Explain the code chunk below. Based on its output, write a model formula with parameter estimates.
landsALL is a categorical variable with the following two levels:
0: no landscape features1: some landscape features
linear_reg() %>% set_engine("lm") %>% fit(Height_in ~ factor(landsALL), data = pp) %>% tidy()## # A tibble: 2 × 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 22.7 0.328 69.1 0 ## 2 factor(landsALL)1 -5.65 0.532 -10.6 7.97e-26Quiz
Q - Explain the code chunk below. Based on its output, write a model formula with parameter estimates.
landsALL is a categorical variable with the following two levels:
0: no landscape features1: some landscape features
linear_reg() %>% set_engine("lm") %>% fit(Height_in ~ factor(landsALL), data = pp) %>% tidy()## # A tibble: 2 × 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 22.7 0.328 69.1 0 ## 2 factor(landsALL)1 -5.65 0.532 -10.6 7.97e-26ˆheighti=22.7−5.65×landsALL
Quiz
Q - Interpret slope and intercept estimates in the context of data.
ˆheighti=22.7−5.65×landsALL
Quiz
Q - Interpret slope and intercept estimates in the context of data.
ˆheighti=22.7−5.65×landsALL
Slope: Paintings with landscape features are expected, on average, to be 5.65 inches shorter than paintings that without landscape features.
- Compares baseline level (
landsALL = 0) to the other level (landsALL = 1) - Q - How do you know which one is the baseline level?
- Compares baseline level (
- Intercept: Paintings that don't have landscape features are expected, on average, to be 22.7 inches tall.
Quiz
Q - What happens in model fitting if a categorical variable has more than two levels?
Quiz
Q - What happens in model fitting if a categorical variable has more than two levels?
- They are automatically encoded to dummy variables (e.g., 6 dummies for 7 levels).
- Each coefficient describes the expected difference by the level compared to the baseline level.
Quiz
Q - Explain the code chunk below.
school_pntg is a categorical variable about school of paintings with 7 levels:
A: Austrian, D\FL: Dutch/Flemish, F: French, G: German, I: Italian, S: Spanish, X: Unknown
linear_reg() %>% set_engine("lm") %>% fit(Height_in ~ school_pntg, data = pp) %>% tidy()## # A tibble: 7 × 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 14.0 10.0 1.40 0.162 ## 2 school_pntgD/FL 2.33 10.0 0.232 0.816 ## 3 school_pntgF 10.2 10.0 1.02 0.309 ## 4 school_pntgG 1.65 11.9 0.139 0.889 ## 5 school_pntgI 10.3 10.0 1.02 0.306 ## 6 school_pntgS 30.4 11.4 2.68 0.00744## # … with 1 more rowQuiz
Q - Interpret slope and intercept estimates in the context of data.
school_pntg is a categorical variable about school of paintings with 7 levels:
A: Austrian, D\FL: Dutch/Flemish, F: French, G: German, I: Italian, S: Spanish, X: Unknown
## # A tibble: 7 × 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 14.0 10.0 1.40 0.162 ## 2 school_pntgD/FL 2.33 10.0 0.232 0.816 ## 3 school_pntgF 10.2 10.0 1.02 0.309 ## 4 school_pntgG 1.65 11.9 0.139 0.889 ## 5 school_pntgI 10.3 10.0 1.02 0.306 ## 6 school_pntgS 30.4 11.4 2.68 0.00744## # … with 1 more rowQuiz
Q - Interpret slope and intercept estimates in the context of data.
school_pntg is a categorical variable about school of paintings with 7 levels:
A: Austrian, D\FL: Dutch/Flemish, F: French, G: German, I: Italian, S: Spanish, X: Unknown
## # A tibble: 7 × 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 14.0 10.0 1.40 0.162 ## 2 school_pntgD/FL 2.33 10.0 0.232 0.816 ## 3 school_pntgF 10.2 10.0 1.02 0.309 ## 4 school_pntgG 1.65 11.9 0.139 0.889 ## 5 school_pntgI 10.3 10.0 1.02 0.306 ## 6 school_pntgS 30.4 11.4 2.68 0.00744## # … with 1 more row- Intercept: Austrian school (A) paintings are expected, on average, to be 14 inches tall.
- Slope: French school (F) paintings are expected, on average, to be 10.2 inches taller than Austrian school paintings.
- Q - How do you know which one is the baseline level?
Bulletin
Watch videos for Prepare: June 10
Lab07 due Friday, June 10 at 11:59pm
HW04 released
Don't forget HW02! It's due Thursday, June 16 at 11:59pm.
Project draft due Monday, June 13 at 11:59pm
Submit
ae20(~ Part 2 Question 2)