Models with Multiple Predictors 2 + Model Diagnostics
Bora Jin
Today's Goal
- Use functions in
Rto fit a linear model with multiple predictors - Model interactions between variables
- Understand what's linear in linear regressions
- Understand and implement CI and HT for regression parameters
- Understand model diagnostics and how to handle common model violations
Quiz
Suppose a dataset called mydata has variables y, x1, and x2. The variable x1 is numeric and x2 is categorical. For the following questions, write out a regression model and the code to fit the model.
Q - Same slope and same intercept between x1 and y for different levels of x2.
Quiz
Suppose a dataset called mydata has variables y, x1, and x2. The variable x1 is numeric and x2 is categorical. For the following questions, write out a regression model and the code to fit the model.
Q - Same slope and same intercept between x1 and y for different levels of x2.
y=β0+β1 x1+ϵ
Quiz
Suppose a dataset called mydata has variables y, x1, and x2. The variable x1 is numeric and x2 is categorical. For the following questions, write out a regression model and the code to fit the model.
Q - Same slope and same intercept between x1 and y for different levels of x2.
y=β0+β1 x1+ϵ
lm(y ~ x1, data = mydata)Quiz
Q - Same slope and different intercept (parallel lines) for different levels of x2.
Quiz
Q - Same slope and different intercept (parallel lines) for different levels of x2.
y=β0+β1 x1+β2 x2+ϵ
Quiz
Q - Same slope and different intercept (parallel lines) for different levels of x2.
y=β0+β1 x1+β2 x2+ϵ
linear_reg(engine = "lm") %>% fit(y ~ x1 + x2, data = mydata)Quiz
Q - Different slope and different intercept (non-parallel lines) for different levels of x2.
Quiz
Q - Different slope and different intercept (non-parallel lines) for different levels of x2.
y=β0+β1 x1+β2 x2+β3 (x1∗x2)+ϵ
Quiz
Q - Different slope and different intercept (non-parallel lines) for different levels of x2.
y=β0+β1 x1+β2 x2+β3 (x1∗x2)+ϵ
lm(y ~ x1*x2, data = mydata)lm(y ~ x1 + x2 + x1:x2, data = mydata)Quiz
Q - Write separate fitted models for non-living artists (artistliving = 0) and for living artists (artistliving = 1) using the following result. Your fitted models should include log_price and surface only.
ˆlog_price=4.91+0.00021 surface−0.126 artistliving + 0.00048 surface∗artistliving
Quiz
Q - Write separate fitted models for non-living artists (artistliving = 0) and for living artists (artistliving = 1) using the following result. Your fitted models should include log_price and surface only.
ˆlog_price=4.91+0.00021 surface−0.126 artistliving + 0.00048 surface∗artistliving
- Non-living artists: ˆlog_price=4.91+0.00021 surface
- Living artists: ˆlog_price=4.784+0.00069 surface
- Non-parallel lines due to the interaction effect!
Model Diagnostics
Source: Duke STA210 by Prof. Mine Çetinkaya-Rundel https://sta210-s22.github.io/website/slides/lec-7.html#
Model Conditions
- Linearity: There is a linear relationship between the response and predictor variables.
- Independence: The errors are independent from each other.
- Normality (optional): The errors follow a normal distribution.
- Equal variance: The variability of the errors is equal for all values of the predictor variable.
- For multiple regression, the predictors should not be too correlated with each other.
Linearity and Equal Variance
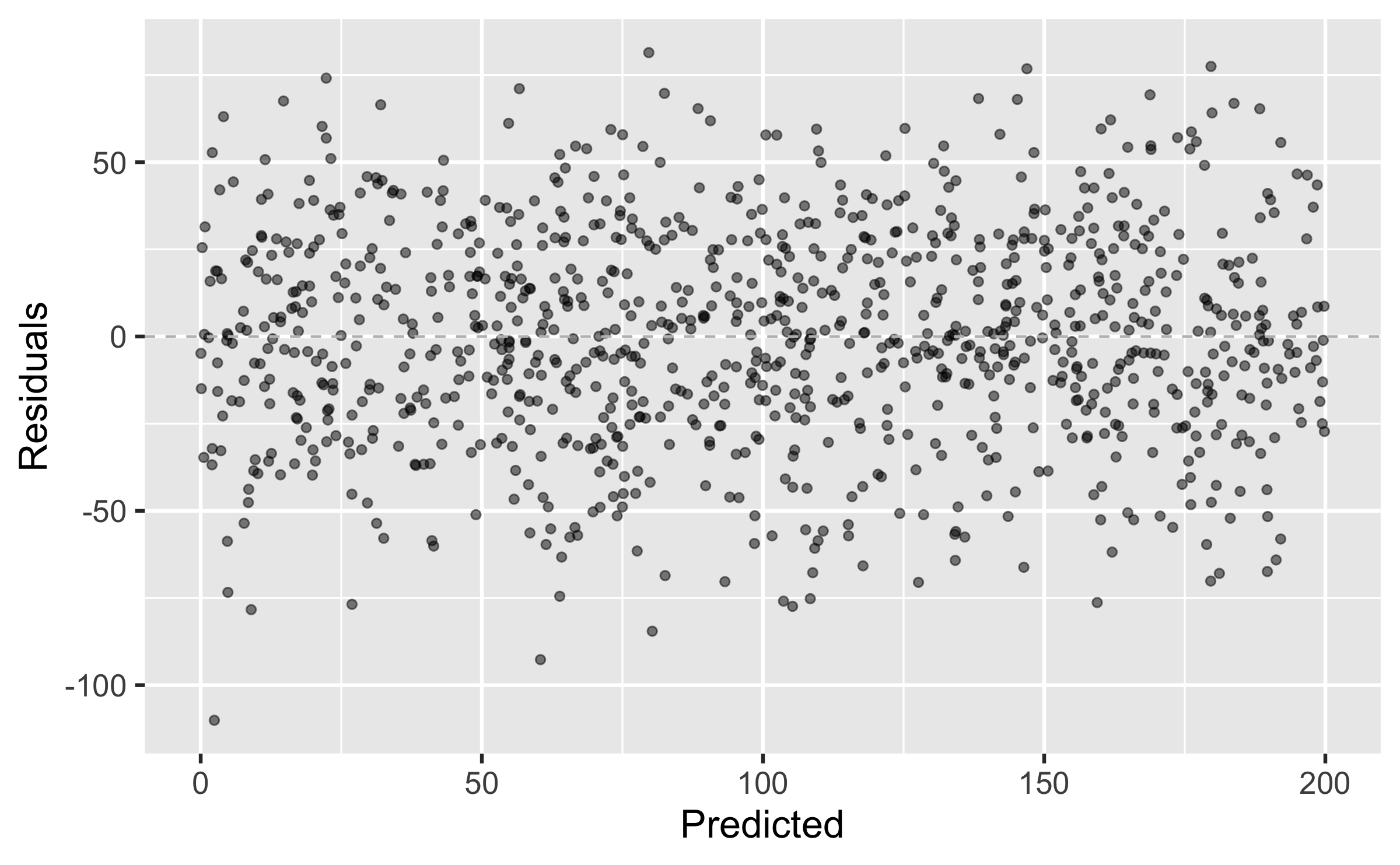
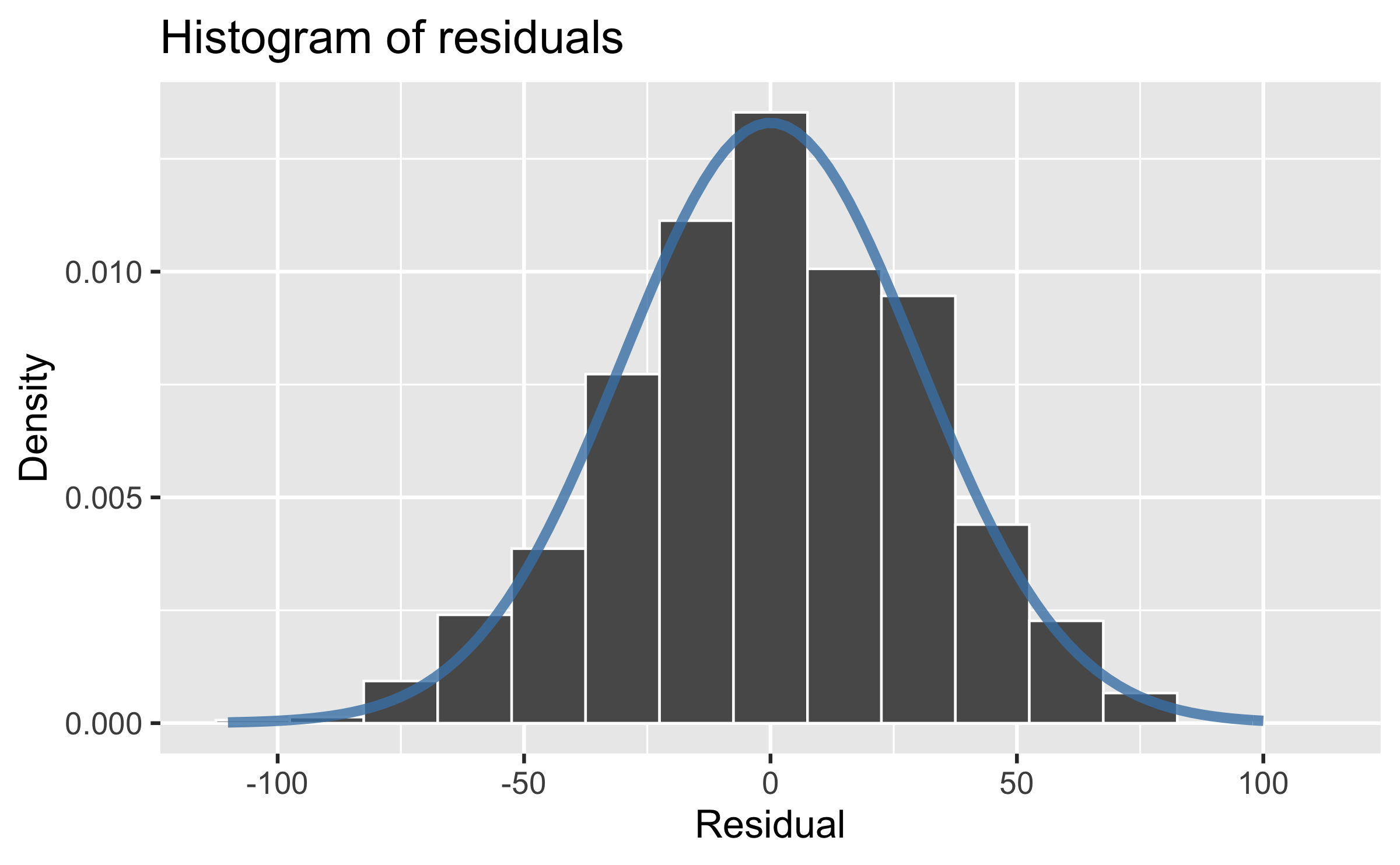
Linearity: The residuals vs. fitted values plot should show a random scatter of residuals around 0.
- No distinguishable pattern or structure along the x or y axes.
Why do we want a complete random scatter?
- It means that my model is good and captures any interesting (linear) relationship in the data.
- Remaining patterns in residuals vs. fitted values suggest that the linear model is not the best assumption for the data.
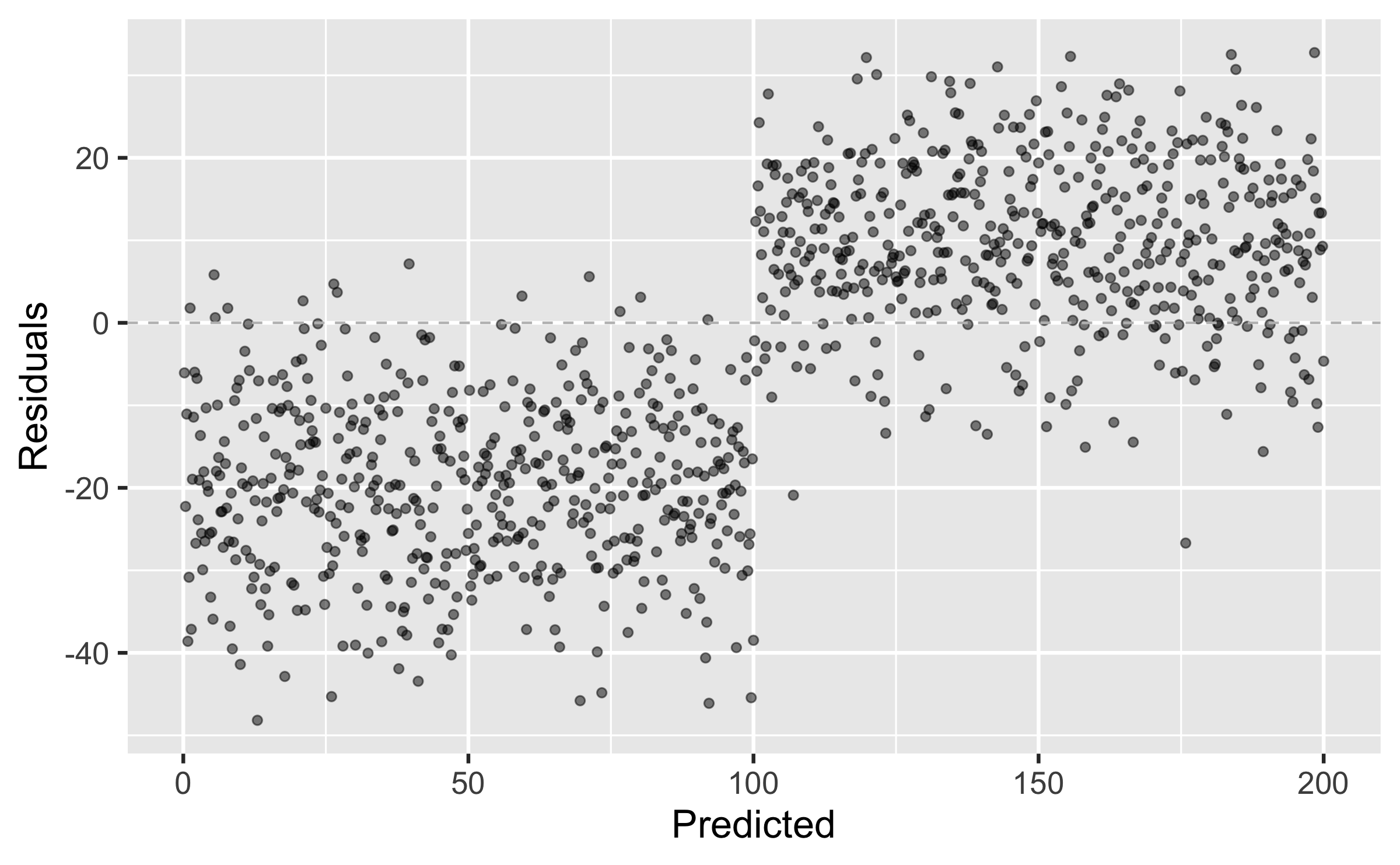
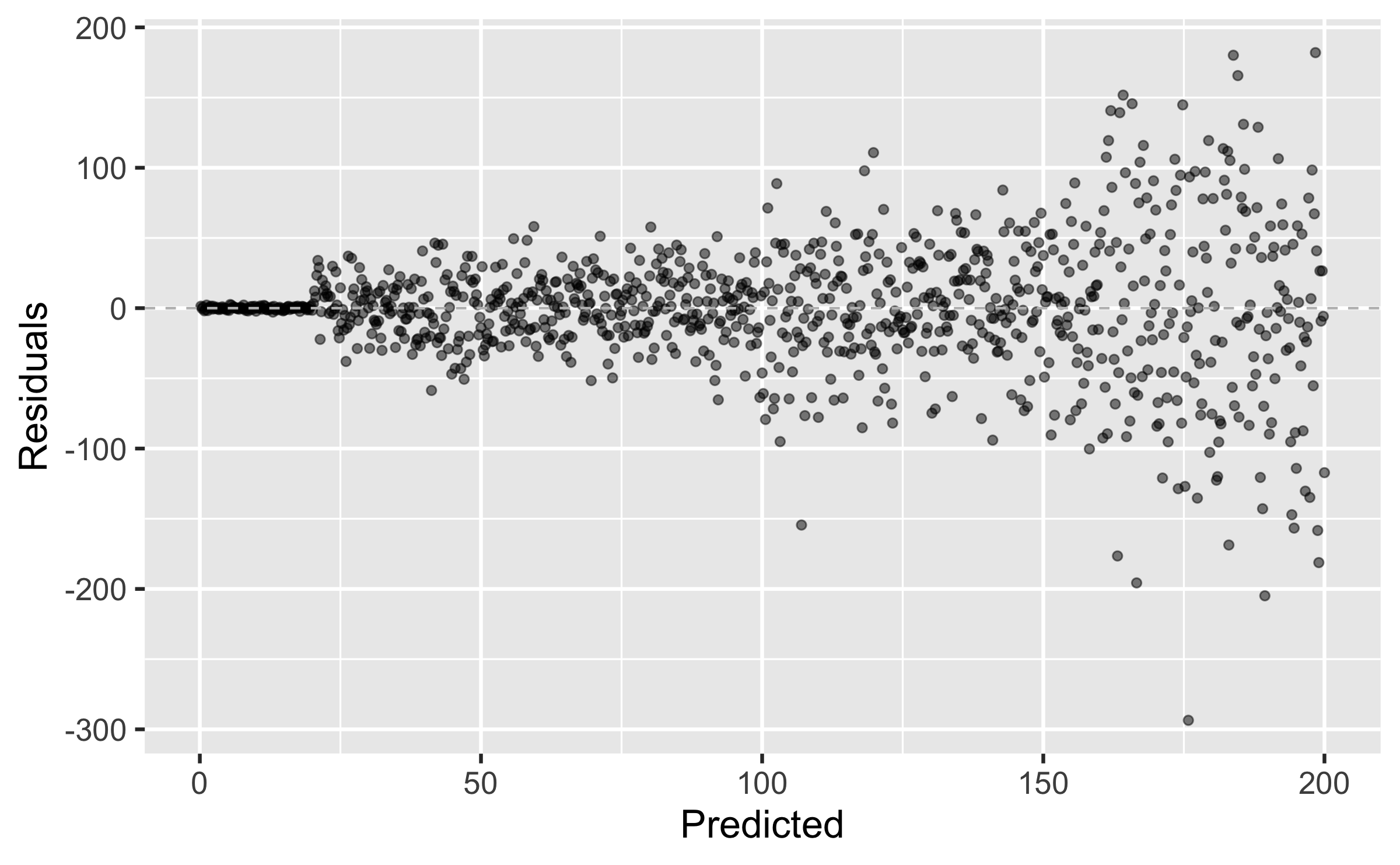
Equal variance: The vertical spread of the residuals should be relatively constant across the plot.
Linearity and Equal Variance
We don't want
increasing / decreasing variability in residuals as predicted value increases
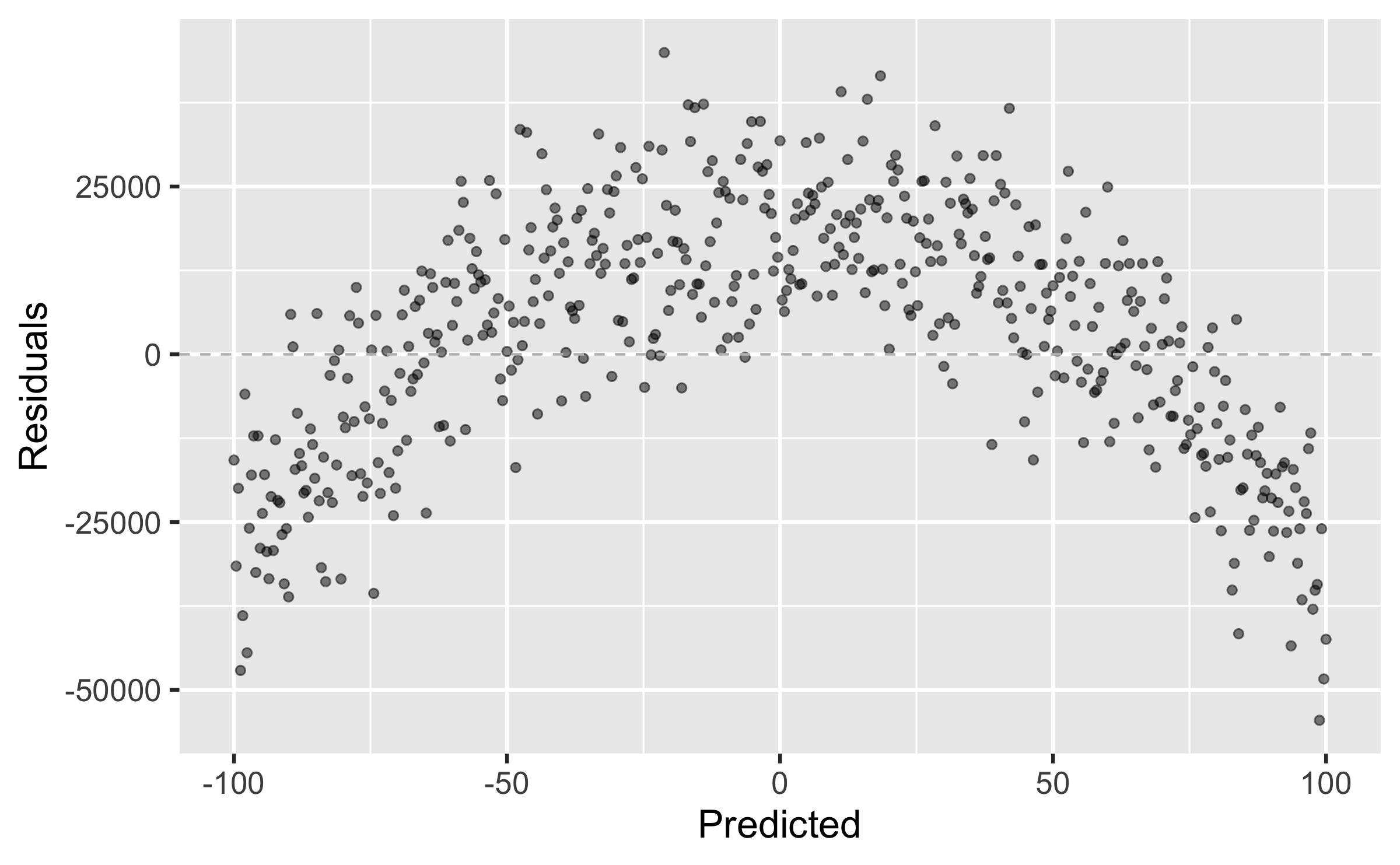
Linearity and Equal Variance
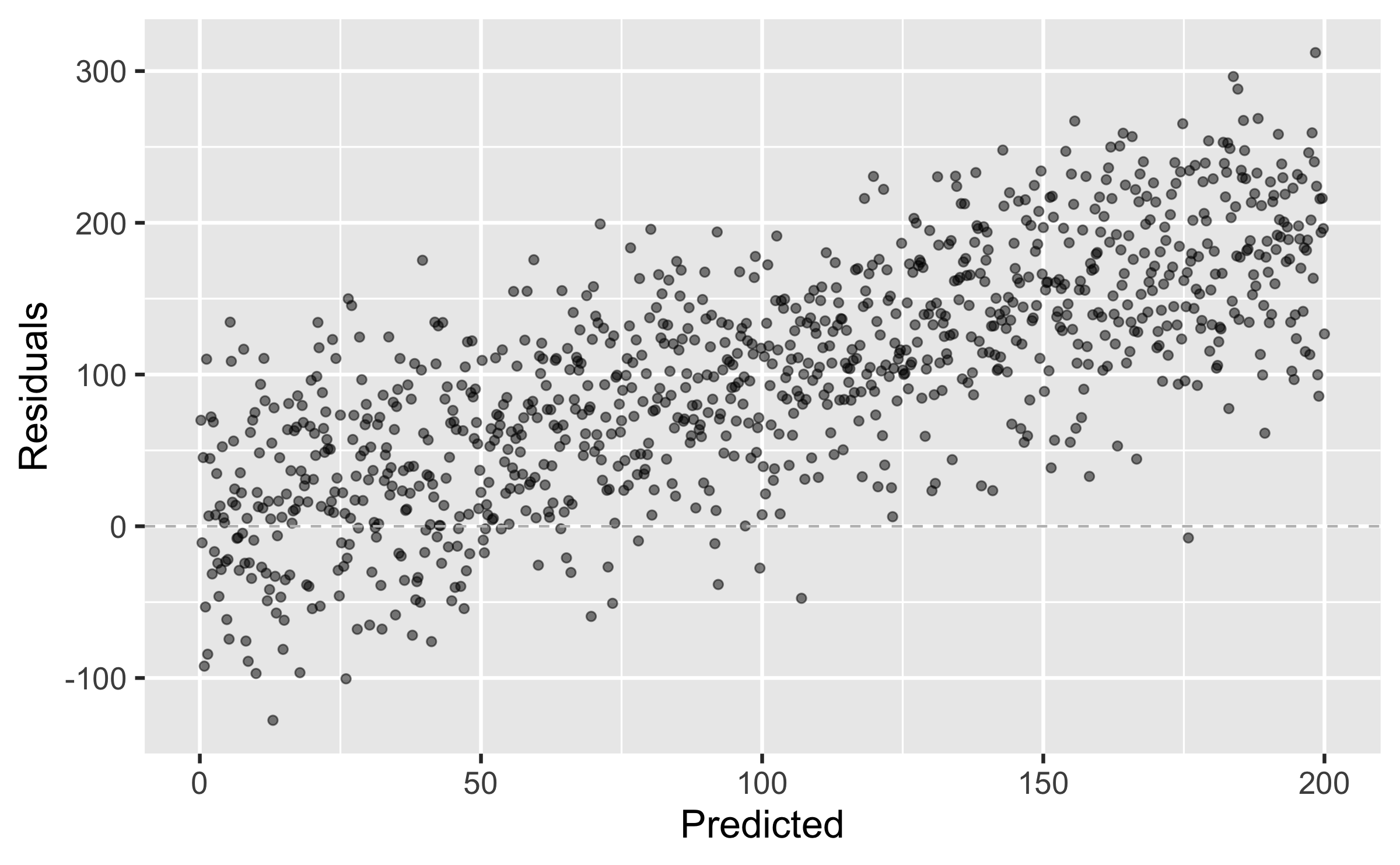
We don't want
residuals correlated with predicted values
Independence
We can often check the independence assumption based on the context of the data and how the observations were collected.
If the data were collected in a particular order, examine a scatterplot of the residuals versus order in which the data were collected.
When Model Conditions Are Violated
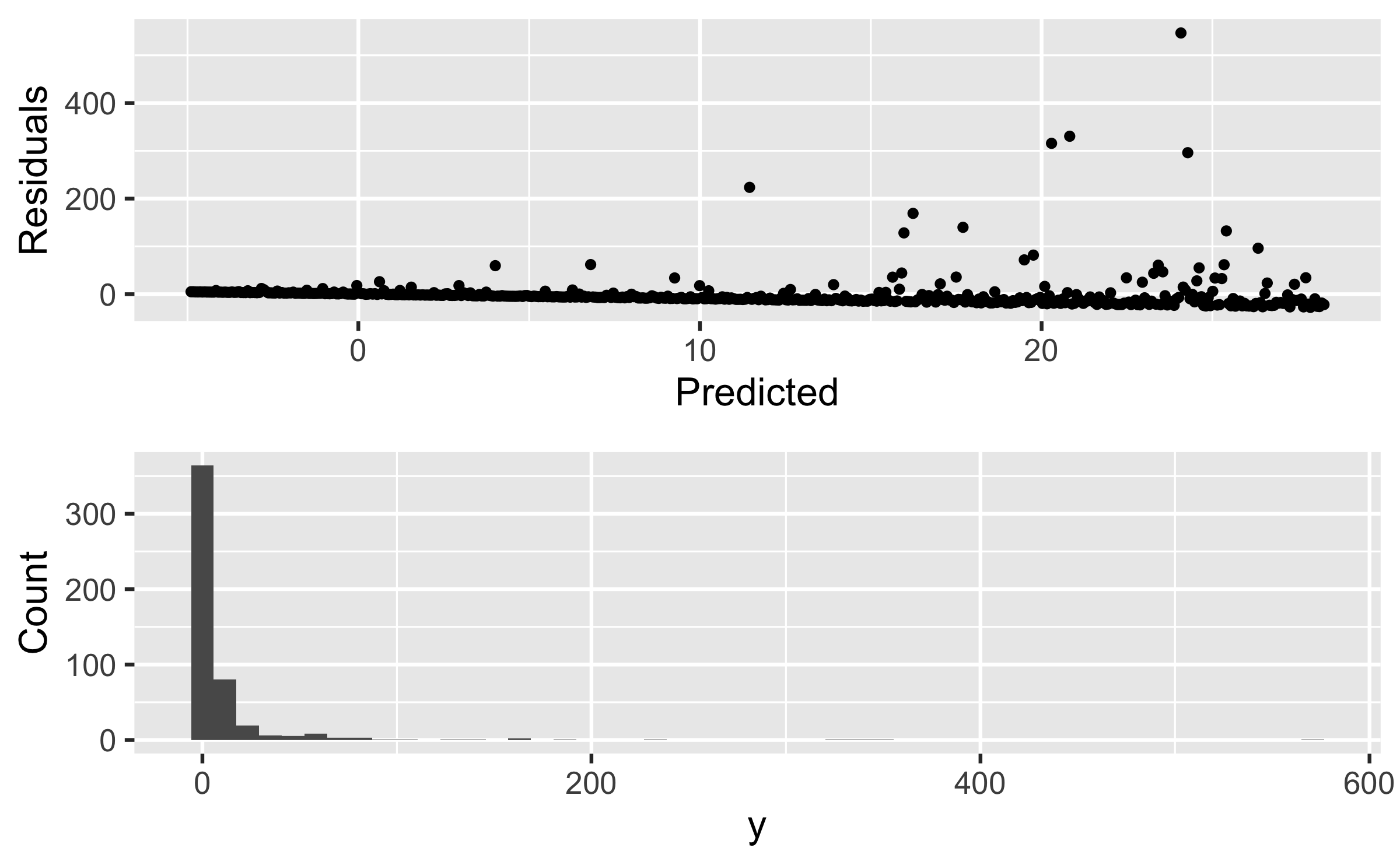
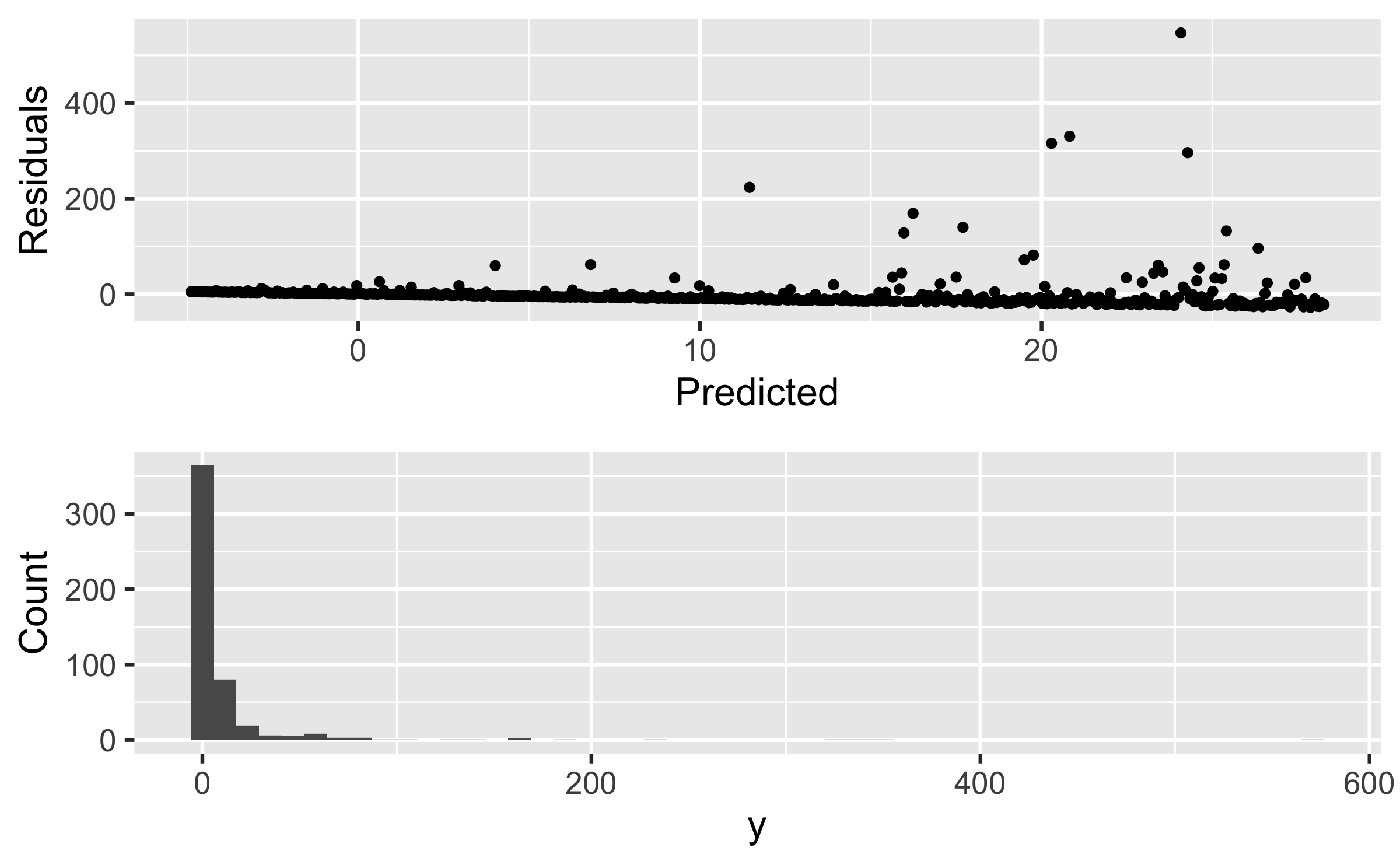
Transform the response variable. This may help!
- Natural log transformation on y variable: In
R,log(y) - Helpful for extremely right skewed distribution and/or non-constant variance in residuals
Log Transformation
This is still a linear model with log(y) as the response: log(y)=β0+β1 x+ϵ ⇒ ˆlog(y)=^β0+^β1 x
logy <- log(y)lm2 <- lm(logy ~ x)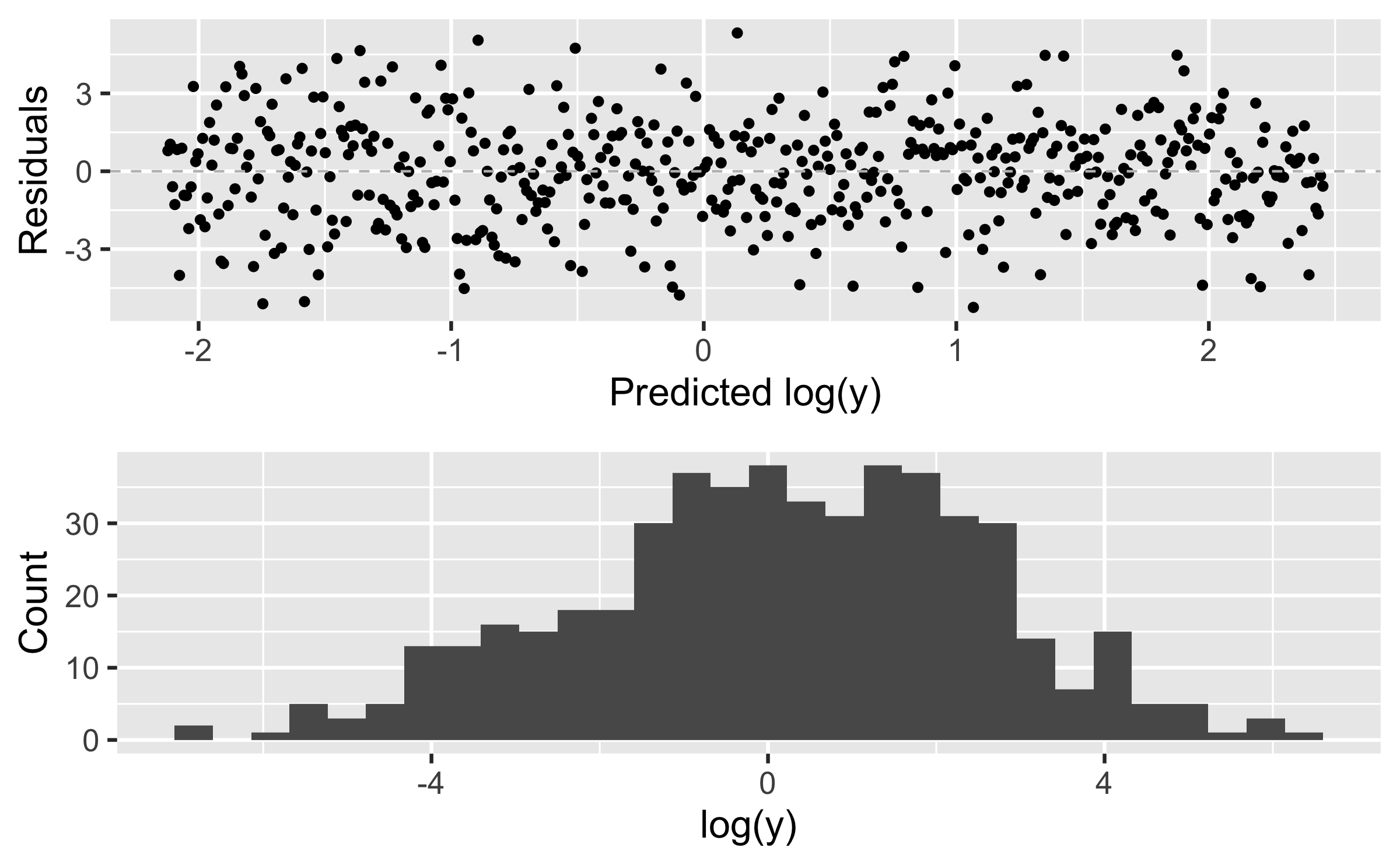
Bulletin
Watch videos for Prepare: June 14
Project draft due tonight at 11:59pm
HW02, HW04 due Thursday, June 16 at 11:59pm
Submit Part 1 and Part 2 of
ae22